题目内容
已知一工厂生产某原料的生产成本y（万元）为产量x（千吨）之间的关系为y=x+
，则生产成本最少时该工厂的产量x为（ ）
| 400 |
| x+1 |
| A、17千吨 | B、18千吨 |
| C、19千吨 | D、20千吨 |
考点：基本不等式在最值问题中的应用
专题：应用题,不等式的解法及应用
分析：利用题意得出y=x+
=（x+1）+
-1，x≥0，转化为，y=t+
-1，t≥1，利用基本不等式求解．
| 400 |
| x+1 |
| 400 |
| x+1 |
| 400 |
| t |
解答：
解：根据题意可得：y=x+
，求解其最小值即可．
∴y=x+
=（x+1）+
-1，x≥0，
设x+1=t，t≥1，y=t+
-1，t≥1，
∵t+
≥2
=40，（t仅当=20等号成立），
∴当x=19时，生产成本最少为40-1=39，
故选：C
| 400 |
| x+1 |
∴y=x+
| 400 |
| x+1 |
| 400 |
| x+1 |
设x+1=t，t≥1，y=t+
| 400 |
| t |
∵t+
| 400 |
| t |
| 400 |
∴当x=19时，生产成本最少为40-1=39，
故选：C
点评：本题考查了函数在实际问题中的应用，结合基本不等式求解，数中档题．
练习册系列答案
相关题目
若一个三角形，采用斜二测画法作出其直观图，则其直观图的面是原三角形面积的（ ）
A、
| ||||
| B、2倍 | ||||
C、
| ||||
D、
|
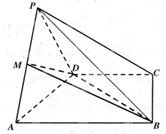如图，四棱锥P-ABCD中，底面ABCD是直角梯形，AB∥CD，∠DAB=60°，AB=AD=2CD=2，侧面PAD⊥底面ABCD，且△PAD为等腰直角三角形，∠APD=90°，M为AP的中点．
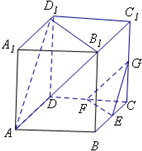如图，在正方体ABCD=A1B1C1D1中，E、F、G分别是CB、CD、CC1的中点．