题目内容
已知函数f(x)=x3+3x2+ax+a
(1)若f(x)在区间(1,2)上单调,求实数a的取值范围;
(2)求证:函数f(x)图象的对称中心是(-1,2).
(1)若f(x)在区间(1,2)上单调,求实数a的取值范围;
(2)求证:函数f(x)图象的对称中心是(-1,2).
考点:利用导数研究函数的单调性
专题:计算题,证明题,导数的综合应用
分析:(1)求导,f(x)在区间(1,2)上单调可化为在(1,2)上“f′(x)≥0恒成立”或“f′(x)≤0恒成立”,从而求解.
(2)在y=f(x)的图象上任取点(x0,y0),其关于(-1,2)的对称点为(x,y);证明(x,y)也在y=f(x)的图象上即可.
(2)在y=f(x)的图象上任取点(x0,y0),其关于(-1,2)的对称点为(x,y);证明(x,y)也在y=f(x)的图象上即可.
解答:
解:(1)f′(x)=3x2+6x+a=3(x+1)2+a-3,
若f(x)在区间(1,2)上单调,
则在(1,2)上“f′(x)≥0恒成立”或“f′(x)≤0恒成立”,
∴f′(1)=9+a≥0或f′(2)=24+a≤0,
即a≤-24或a≥-9.
(2)证明:在y=f(x)的图象上任取点(x0,y0),其关于(-1,2)的对称点为(x,y);
则
,即
;
则4-y=(-2-x)3+3(-2-x)2+a(-2-x)+a,
整理可得,y=x3+3x2+ax+a,
∴y=f(x)的图象关于(-1,2)对称的曲线方程仍为y=f(x),
即函数f(x)图象的对称中心是(-1,2).
若f(x)在区间(1,2)上单调,
则在(1,2)上“f′(x)≥0恒成立”或“f′(x)≤0恒成立”,
∴f′(1)=9+a≥0或f′(2)=24+a≤0,
即a≤-24或a≥-9.
(2)证明:在y=f(x)的图象上任取点(x0,y0),其关于(-1,2)的对称点为(x,y);
则
|
|
则4-y=(-2-x)3+3(-2-x)2+a(-2-x)+a,
整理可得,y=x3+3x2+ax+a,
∴y=f(x)的图象关于(-1,2)对称的曲线方程仍为y=f(x),
即函数f(x)图象的对称中心是(-1,2).
点评:本题考查了导数的综合应用,同时考查了图象的对称性,属于中档题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
已知两条相交直线a、b,a∥平面α,则b与平面α的位置关系( )
| A、b∥α |
| B、b与α相交 |
| C、b?α |
| D、b∥α或b与α相交 |
已知一工厂生产某原料的生产成本y(万元)为产量x(千吨)之间的关系为y=x+
,则生产成本最少时该工厂的产量x为( )
| 400 |
| x+1 |
| A、17千吨 | B、18千吨 |
| C、19千吨 | D、20千吨 |
设M(x,y)是区域
内的动点,且不等式x+2y≤14恒成立,则实数a的取值范围是( )
|
| A、[8,10] |
| B、[8,9] |
| C、[6,9] |
| D、[6,10] |
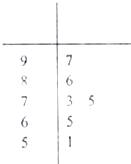 某校高一级数学必修一模块考试的成绩分为四个等级,85分-100分为A等,70分-84分为B等,55分-69分为C等,54分以下为D等.右边的茎叶图(十位为茎,个位为叶)记录了某班某小组6名学生的数学必修一模块考试成绩.
某校高一级数学必修一模块考试的成绩分为四个等级,85分-100分为A等,70分-84分为B等,55分-69分为C等,54分以下为D等.右边的茎叶图(十位为茎,个位为叶)记录了某班某小组6名学生的数学必修一模块考试成绩.