题目内容
复数z是方程z2+2z+2=0的解,若Imz>0,且
-
=b+bi(a,b∈R+),则
+
的最小值为 .
| a |
| z |
. |
| z |
| 1 |
| a |
| 1 |
| b |
考点:复数相等的充要条件,基本不等式,复数代数形式的乘除运算
专题:数系的扩充和复数
分析:由题意,复数z是方程z2+2z+2=0的解,且 Imz>0,由此方程解出符合条件的z,再代入
-
=b+bi,由复数相等的条件求得a,b的关系,然后利用基本不等式求最值.
| a |
| z |
. |
| z |
解答:
解:方程z2+2z+2=0的解z=-1±i,
∵Imz>0,
∴z=-1+i,
将z=-1+i代入
-
=b+bi,得
+1+i=b+bi,
∴
+1+i=b+bi,
(-
+1)+(-
+1)i=b+bi,
∴-
+1=b,
+b=1.
则
+
=(
+
)(
+b)=
+1+
+
≥
+2
=
+
.
当且仅当
,即a=2
-2,b=2-
时上式等号成立.
故答案为:
+
.
∵Imz>0,
∴z=-1+i,
将z=-1+i代入
| a |
| z |
. |
| z |
| a |
| -1+i |
∴
| a(-1-i) |
| (-1+i)(-1-i) |
(-
| a |
| 2 |
| a |
| 2 |
∴-
| a |
| 2 |
| a |
| 2 |
则
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
| a |
| 2 |
| 1 |
| 2 |
| b |
| a |
| a |
| 2b |
| 3 |
| 2 |
|
| 3 |
| 2 |
| 2 |
当且仅当
|
| 2 |
| 2 |
故答案为:
| 3 |
| 2 |
| 2 |
点评:本题考查了复数代数形式的乘除运算,考查了复数相等的条件,训练了利用基本不等式求最值,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
命题“?x∈R,使得x2+x+1<0”的否定是( )
| A、?x∈R,均有x2+x+1<0 |
| B、?x∈R,均有x2+x+1≥0 |
| C、?x∈R,使得 x2+x+1<0 |
| D、?x∈R,均有x2+x+1<0 |
已知一工厂生产某原料的生产成本y(万元)为产量x(千吨)之间的关系为y=x+
,则生产成本最少时该工厂的产量x为( )
| 400 |
| x+1 |
| A、17千吨 | B、18千吨 |
| C、19千吨 | D、20千吨 |
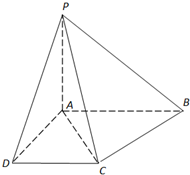 如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.
如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.