题目内容
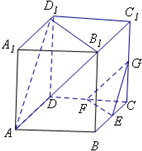 如图,在正方体ABCD=A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点.
如图,在正方体ABCD=A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点.(1)求证:AD1∥平面EFG;
(2)求证:平面AB1D1∥平面EFG;
(3)求异面直线B1D1与EG所成的角度数.
考点:异面直线及其所成的角,直线与平面平行的判定,平面与平面平行的判定
专题:空间位置关系与距离
分析:(1)首先,连结C1B,然后,得到四边形ABC1D1是平行四边形,从而得证;
(2)根据(1)可以证明AB1∥平面EFG,从而证明;
(3)根据平行关系,得到∠FEG就是异面直线B1D1与EG所成的角,然后放到三角形中求解.
(2)根据(1)可以证明AB1∥平面EFG,从而证明;
(3)根据平行关系,得到∠FEG就是异面直线B1D1与EG所成的角,然后放到三角形中求解.
解答:
解:(1)连结C1B,
∵AB∥B1C1,且AB=B1C1
∴四边形ABC1D1是平行四边形,
∴AD1∥BC1,
又∵E、G为中点,
∴BC1∥EG,
∴AD1∥EG,
∴AD1∥平面EFG;
(2)结合(1),同理可以证明
AB1∥平面EFG,
∵AB1∩AD1=A,
∴平面AB1D1∥平面EFG;
(3)∵BD∥B1D1,且BD∥EF,
∴∠FEG就是异面直线B1D1与EG所成的角,
在△EFG中,显然为等边三角形,
∴异面直线B1D1与EG所成的角为60°.
∵AB∥B1C1,且AB=B1C1
∴四边形ABC1D1是平行四边形,
∴AD1∥BC1,
又∵E、G为中点,
∴BC1∥EG,
∴AD1∥EG,
∴AD1∥平面EFG;
(2)结合(1),同理可以证明
AB1∥平面EFG,
∵AB1∩AD1=A,
∴平面AB1D1∥平面EFG;
(3)∵BD∥B1D1,且BD∥EF,
∴∠FEG就是异面直线B1D1与EG所成的角,
在△EFG中,显然为等边三角形,
∴异面直线B1D1与EG所成的角为60°.
点评:本题重点考查了空间中平行关系、异面直线所成的角等知识,考查比较综合,解题关键是学会转化思想在立体几何中的应用.

练习册系列答案
相关题目
已知一工厂生产某原料的生产成本y(万元)为产量x(千吨)之间的关系为y=x+
,则生产成本最少时该工厂的产量x为( )
| 400 |
| x+1 |
| A、17千吨 | B、18千吨 |
| C、19千吨 | D、20千吨 |
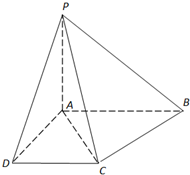 如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.
如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.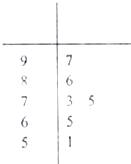 某校高一级数学必修一模块考试的成绩分为四个等级,85分-100分为A等,70分-84分为B等,55分-69分为C等,54分以下为D等.右边的茎叶图(十位为茎,个位为叶)记录了某班某小组6名学生的数学必修一模块考试成绩.
某校高一级数学必修一模块考试的成绩分为四个等级,85分-100分为A等,70分-84分为B等,55分-69分为C等,54分以下为D等.右边的茎叶图(十位为茎,个位为叶)记录了某班某小组6名学生的数学必修一模块考试成绩.