题目内容
设A(1,2),B(3,-1),C(3,4),则
•
( )
| AB |
| AC |
| A、11 | B、5 | C、-2 | D、1 |
考点:平面向量数量积的运算,平面向量的坐标运算
专题:计算题,平面向量及应用
分析:运用向量的坐标运算和向量的数量积的坐标表示,计算即可得到所求值.
解答:
解:由A(1,2),B(3,-1),C(3,4),
则
=(2,-3),
=(2,2),
则
•
=2•2+(-3)•2=-2.
故选C.
则
| AB |
| AC |
则
| AB |
| AC |
故选C.
点评:本题考查向量的坐标运算,主要考查向量的数量积的坐标表示,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
利用“五点法”作出下列函数的简图,并分别说明每个函数的图象与函数y=sinx的图象有什么关系.
(1)y=
sinx;
(2)y=4sinx;
(3)y=sin(x+
);
(4)y=sin(x-
).
(1)y=
| 1 |
| 3 |
(2)y=4sinx;
(3)y=sin(x+
| π |
| 6 |
(4)y=sin(x-
| π |
| 4 |
已知f(x)是定义在R上的奇函数,当0≤x≤1时,f(x)=x2,当x>0时,f(x+1)=f(x)+1,若直线y=kx与函数y=f(x)的图象恰有9个不同的公共点,则实数k的值为( )
A、2
| ||
B、2
| ||
C、2
| ||
D、2
|
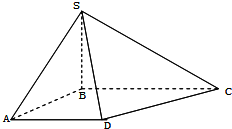 如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AB垂直于AD和BC,侧棱SB⊥平面ABCD,且SB=AB=AD=1,BC=2.
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AB垂直于AD和BC,侧棱SB⊥平面ABCD,且SB=AB=AD=1,BC=2.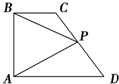 如图,在直角梯形ABCD中,已知BC∥AD,AB⊥AD,AB=4,BC=2,AD=4,若P为CD的中点,则
如图,在直角梯形ABCD中,已知BC∥AD,AB⊥AD,AB=4,BC=2,AD=4,若P为CD的中点,则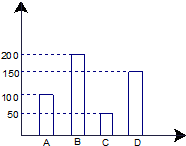 某工厂2014年第一季度生产的A、B、C、D四种型号的产品产量用条形图表示如图,现用分层抽样的方法从中选取50件样品参加四月份的一个展销会.
某工厂2014年第一季度生产的A、B、C、D四种型号的产品产量用条形图表示如图,现用分层抽样的方法从中选取50件样品参加四月份的一个展销会.