题目内容
已知O为△ABC外一点，D为BC边上一点，且
+
-2
=0，若AB=3，AC=5．则
•
=（ ）
| OC |
| OB |
| OD |
| AD |
| BC |
| A、-8 | B、8 | C、-2 | D、2 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由题意和向量的加法运算判断出D是BC的中点，由向量的加法、减法运算、向量的数量积化简
•
即可．
| AD |
| BC |
解答：
解：由题意知，
+
-2
=0，则
+
=2
，
所以D是BC的中点，
又AB=3，AC=5，
则
•
=
（
+
）•（
-
）=
（
2-
2）
=
（25-9）=8，
故选：B．
| OC |
| OB |
| OD |
| OC |
| OB |
| OD |
所以D是BC的中点，
又AB=3，AC=5，
则
| AD |
| BC |
| 1 |
| 2 |
| AC |
| AB |
| AC |
| AB |
| 1 |
| 2 |
| AC |
| AB |
=
| 1 |
| 2 |
故选：B．
点评：本题考查向量的加、减法运算及其几何意义，以及向量数量积的运算，解题的关键是抓住向量的之间的关系，再结合已知条件化简．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
已知sinα＞sinβ，α∈（-
，0），β∈（π，
π），则（ ）
| π |
| 2 |
| 3 |
| 2 |
| A、α+β＞π | ||
| B、α+β＜π | ||
C、α-β≥-
| ||
D、α-β≤-
|
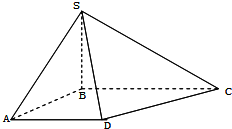如图，在四棱锥S-ABCD中，底面ABCD是直角梯形，AB垂直于AD和BC，侧棱SB⊥平面ABCD，且SB=AB=AD=1，BC=2．
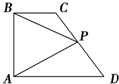如图，在直角梯形ABCD中，已知BC∥AD，AB⊥AD，AB=4，BC=2，AD=4，若P为CD的中点，则
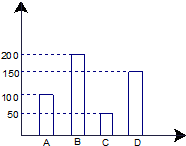某工厂2014年第一季度生产的A、B、C、D四种型号的产品产量用条形图表示如图，现用分层抽样的方法从中选取50件样品参加四月份的一个展销会．已知f（x）是定义在R上的奇函数，当0≤x≤1时，f（x）=x2，当x＞0时，f（x+1）=f（x）+1，若直线y=kx与函数y=f（x）的图象恰有9个不同的公共点，则实数k的值为（ ）
A、2
| ||
B、2
| ||
C、2
| ||
D、2
|
已知向量
=（1，2），
=（2x，-3），若
⊥（
+
），则x=（ ）
| a |
| b |
| a |
| a |
| b |
| A、3 | ||
B、-
| ||
| C、-3 | ||
D、
|