题目内容
15.已知Sn为正项数列{an}的前n项和,且满足$2{S_n}={a_n}^2+{a_n}(n∈{N^*})$.(1)求出a1,a2,a3,a4,
(2)猜想{an}的通项公式并给出证明.
分析 (1)根据Sn=2n-an,利用递推公式,求出a1,a2,a3,a4.
(2)由a1=S1,an=Sn-Sn-1,化简整理,即可得到所求;
解答 解:(1)由Sn=$\frac{1}{2}$an2+$\frac{1}{2}$an(n∈N+).
可得a1=$\frac{1}{2}$a12+$\frac{1}{2}$a1,解得a1=1,S2=a1+a2=$\frac{1}{2}$a22+$\frac{1}{2}$a2,解得a2=2,
同理a3=3,a4=4,
(2)由(1)猜想an=n.
证明:由Sn=$\frac{1}{2}$an2+$\frac{1}{2}$an①
当n≥2时,Sn-1=$\frac{1}{2}$an-12+$\frac{1}{2}$an-1,②
①-②得(an-an-1-1)(an+an-1)=0,
∵an+an-1≠0,∴an-an-1=1,又a1=1,
故数列{an}是首项a1=1,公差d=1的等差数列,故an=n.
点评 本题考查了数列的递推公式,考查了学生的运算能力和转化能力,属于中档题.

练习册系列答案
相关题目
10.已知函数$f(x)=sin({ωx+\frac{π}{4}})({ω>0})在({\frac{π}{2},π})$单调递减,则ω的取值范围可以是( )
| A. | $[{\frac{1}{2},\frac{5}{4}}]$ | B. | $[{0,\frac{5}{4}}]$ | C. | $({0,\frac{1}{2}}]$ | D. | (0,2] |
5.下列表示旅客搭乘动车的流程中,正确的是( )
| A. | 买票→候车厅候车→上车→候车检票口检票 | |
| B. | 候车厅候车→买票→上车→候车检票口检票 | |
| C. | 买票→候车厅候车→候车检票口检票→上车 | |
| D. | 候车厅候车→上车→候车检票口检票→买票 |
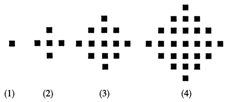 某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.