题目内容
7.已知α∈($\frac{π}{2}$,π),sinα=$\frac{3}{5}$.(1)求sin($\frac{π}{4}$+α)的值;
(2)求cos($\frac{π}{6}$-2α)的值.
分析 (1)由已知利用同角三角函数基本关系式可求cosα的值,进而利用两角和的正弦函数公式即可计算得解.
(2)利用二倍角公式可求sin2α,cos2α的值,进而利用两角差的余弦函数公式即可计算得解.
解答 (本小题满分12 分)
解:(1)∵$α∈({\frac{π}{2}\;,\;π})$,$sinα=\frac{3}{5}$,
∴$cosα=-\sqrt{1-{{sin}^2}α}=-\frac{4}{5}$,…(2分)
∴$sin({\frac{π}{4}+α})=sin\frac{π}{4}cosα+cos\frac{π}{4}sinα=\frac{{\sqrt{2}}}{2}(cosα+sinα)=-\frac{{\sqrt{10}}}{10}$=$-\frac{{\sqrt{2}}}{10}$.…(6分)
(2)∵$sin2α=2sinαcosα=-\frac{24}{25},cos2α={cos^2}α-{sin^2}α=\frac{7}{25}$,…(8分)
∴$cos(\frac{π}{6}-2α)=cos\frac{π}{6}cos2α+sin\frac{π}{6}sin2α$=$\frac{{\sqrt{3}}}{2}×\frac{7}{25}+\frac{1}{2}×(-\frac{24}{25})=\frac{{7\sqrt{3}-24}}{50}$.…(12分)
点评 本题主要考查了同角三角函数基本关系式,两角和的正弦函数公式,二倍角公式,两角差的余弦函数公式在三角函数化简求值中的应用,考查了转化思想,属于基础题.

练习册系列答案
相关题目
4.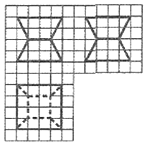 如图,网格纸上小正方形的边长为1,图中粗线画出的是某零件的三视图,该零件由一个棱长为4的正方体毛坯切削得到,则切削掉部分的体积与原毛坯体积的比值为( )
如图,网格纸上小正方形的边长为1,图中粗线画出的是某零件的三视图,该零件由一个棱长为4的正方体毛坯切削得到,则切削掉部分的体积与原毛坯体积的比值为( )
 如图,网格纸上小正方形的边长为1,图中粗线画出的是某零件的三视图,该零件由一个棱长为4的正方体毛坯切削得到,则切削掉部分的体积与原毛坯体积的比值为( )
如图,网格纸上小正方形的边长为1,图中粗线画出的是某零件的三视图,该零件由一个棱长为4的正方体毛坯切削得到,则切削掉部分的体积与原毛坯体积的比值为( )| A. | $\frac{3}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{5}{12}$ | D. | $\frac{7}{12}$ |
2.已知函数y=3sin($\frac{1}{2}$x-$\frac{π}{4}$)
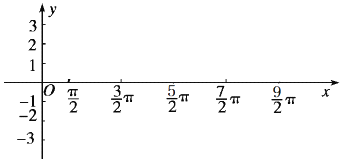
(1)求此函数的振幅、周期和初相;
(2)用五点法在给定的坐标系中作出函数一个周期的图象.(先列表再作图)
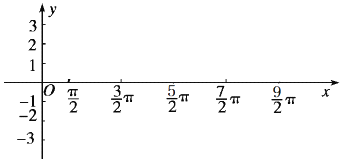
(1)求此函数的振幅、周期和初相;
(2)用五点法在给定的坐标系中作出函数一个周期的图象.(先列表再作图)
| $\frac{1}{2}$x-$\frac{π}{4}$ | |||||
| x | |||||
| 3sin($\frac{1}{2}$x-$\frac{π}{4}$) |
19.某校高二(1)班每周都会选出两位“迟到之星”,期中考试之前一周“迟到之星”人选揭晓之前,小马说:“两个人选应该是在小赵、小宋和小谭三人之中产生”,小赵说:“一定没有我,肯定有小宋”,小宋说:“小马、小谭二人中有且仅有一人是迟到之星”,小谭说:“小赵说的对”.已知这四人中有且只有两人的说法是正确的,则“迟到之星”是( )
| A. | 小赵、小谭 | B. | 小马、小宋 | C. | 小马、小谭 | D. | 小赵、小宋 |
16.已知一只蚂蚁在边长为4的正三角形内爬行,则此蚂蚁到三角形三个顶点的距离均超过1的概率为( )
| A. | $\frac{\sqrt{3}π}{12}$ | B. | $\frac{\sqrt{3}π}{24}$ | C. | 1-$\frac{\sqrt{3}π}{12}$ | D. | 1-$\frac{\sqrt{3}π}{24}$ |
17.已知过原点的直线l1与直线l2:x+3y+1=0垂直,圆C的方程为x2+y2-2ax-2ay=1-2a2(a>0),若直线l1与圆C交于M,N两点,则当△CMN的面积最大时,圆心C的坐标为( )
| A. | $({\frac{{\sqrt{5}}}{2},\frac{{\sqrt{5}}}{2}})$ | B. | $({\frac{{\sqrt{3}}}{2},\frac{{\sqrt{3}}}{2}})$ | C. | $({\frac{1}{2},\frac{1}{2}})$ | D. | (1,1) |