题目内容
3.如果a>b>0,那么下列不等式成立的是( )| A. | $\frac{1}{a}$>$\frac{1}{b}$ | B. | -$\frac{1}{a}$<-$\frac{1}{b}$ | C. | ab<b2 | D. | ab<a2 |
分析 利用不等式的基本性质,转化求解即可.
解答 解:a>b>0,则ab>0,$\frac{1}{ab}>0$,
所以$a•\frac{1}{ab}>b•\frac{1}{ab}$,可得$\frac{1}{b}>\frac{1}{a}$,所以A,B不成立.
a•a>ab>0,即ab<a2,所以C不正确,D正确;
故选:D.
点评 本题考查不等式的基本性质,是基础题.

练习册系列答案
相关题目
14.已知某几何体的三视图如图所示,则该几何体的体积为( )
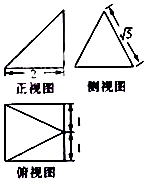

| A. | $\frac{4}{3}$$\sqrt{5}$ | B. | 4$\sqrt{5}$ | C. | $\frac{8}{3}$ | D. | 8 |
11.正整数按如表的规律排列,则第2017行,第2016列的数应为( )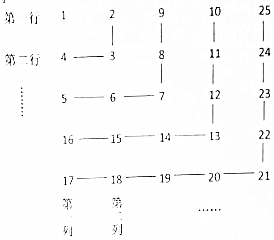

| A. | 20162 | B. | 2016×2017 | C. | 20172 | D. | 2017×2018 |
18.以下是解决数学问题的思维过程的流程图,则( )


| A. | ①综合法②分析法 | B. | ①分析法②综合法 | C. | ①综合法②反证法 | D. | ①分析法②反证法 |
8.观察下列各式:55=3 125,56=15 625,57=78 125,58=390 625,59=1 953 125,…,则585的末四位数字为( )
| A. | 3125 | B. | 5625 | C. | 8125 | D. | 0625 |
12.如图,第n个图形是由正n+2边形“扩展”而来,(n=1、2、3、…),则在第5个图形中共有( )个顶点.


| A. | 48 | B. | 52 | C. | 56 | D. | 60 |
13. 按如图程序框图运算:若运算进行3次才停止,则输入的x的取值范围是( )
按如图程序框图运算:若运算进行3次才停止,则输入的x的取值范围是( )
 按如图程序框图运算:若运算进行3次才停止,则输入的x的取值范围是( )
按如图程序框图运算:若运算进行3次才停止,则输入的x的取值范围是( )| A. | (10,28] | B. | (10,28) | C. | [10,28) | D. | [10,28] |
