题目内容
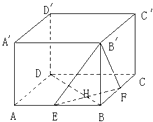 在棱长为a的正方体ABCD-A′B′C′D′中,如图E、F分别为棱AB与BC的中点,EF∩BD=H;
在棱长为a的正方体ABCD-A′B′C′D′中,如图E、F分别为棱AB与BC的中点,EF∩BD=H;(Ⅰ)求二面角B′-EF-B的正切值;
(Ⅱ)试在棱B′B上找一点M,使D′M⊥面EFB′,并证明你的结论.
考点:直线与平面垂直的性质,与二面角有关的立体几何综合题
专题:空间位置关系与距离
分析:(I)连结B′D′,AC,B′H,由已知条件推导出EF⊥平面BB′D′D,从布推导出∠B′HB为二面角B′-EF-B的平面角,由此能求出二面角B′-EF-B的正切值的大小.
(II)在棱B′B上取中点M,连结D′M,则D′M⊥面EFB′.连结CM,由线面垂直得D′M⊥EF.由三垂线定理得B′F⊥D′M,由此能证明D′M⊥面EFB′.
(II)在棱B′B上取中点M,连结D′M,则D′M⊥面EFB′.连结CM,由线面垂直得D′M⊥EF.由三垂线定理得B′F⊥D′M,由此能证明D′M⊥面EFB′.
解答:
解:(I)连结B′D′,AC,B′H,
∵底面ABCD为正方形,∴AC⊥BD,
又∵E,E分别为AB,BC的中点,∴EF∥AC,∴EF⊥BD,
又∵棱B′B⊥底面ABCD,EF?底面ABCD,
∴EF⊥B′B,而B′B∩BD=B,∴EF⊥平面BB′D′D,
又∵B′H?面BB′D′D,BN?面BB′D′D,
∴EF⊥B′H,EF⊥BH,
∴∠B′HB为二面角B′-EF-B的平面角,
在RT△B′BH中,B′B=a,BH=
a,
∴tan∠B′HB=
=2
,
∴二面角B′-EF-B的正切值的大小为2
.
(II)在棱B′B上取中点M,连结D′M,则D′M⊥面EFB′.
证明如下:
连结CM,∵EF⊥面BB′D′D,D′M?面BB′D′D,
∴D′M⊥EF.
又∵D′C′⊥面B′BCC′,∴C′M为D′M在面B′BCC′内的射影.
在正方形B′BCC′中,M,F分别为B′,B和BC的中点,
∴B′F⊥C′M,于是由三垂线定理得B′F⊥D′M,
而B′F?面EFB′,EF?面EFB′,∴EF∩B′F=F,
∴D′M⊥面EFB′.
∵底面ABCD为正方形,∴AC⊥BD,
又∵E,E分别为AB,BC的中点,∴EF∥AC,∴EF⊥BD,
又∵棱B′B⊥底面ABCD,EF?底面ABCD,
∴EF⊥B′B,而B′B∩BD=B,∴EF⊥平面BB′D′D,
又∵B′H?面BB′D′D,BN?面BB′D′D,
∴EF⊥B′H,EF⊥BH,
∴∠B′HB为二面角B′-EF-B的平面角,
在RT△B′BH中,B′B=a,BH=
| ||
| 4 |
∴tan∠B′HB=
| B′B |
| BH |
| 2 |
∴二面角B′-EF-B的正切值的大小为2
| 2 |
(II)在棱B′B上取中点M,连结D′M,则D′M⊥面EFB′.
证明如下:
连结CM,∵EF⊥面BB′D′D,D′M?面BB′D′D,
∴D′M⊥EF.
又∵D′C′⊥面B′BCC′,∴C′M为D′M在面B′BCC′内的射影.
在正方形B′BCC′中,M,F分别为B′,B和BC的中点,
∴B′F⊥C′M,于是由三垂线定理得B′F⊥D′M,
而B′F?面EFB′,EF?面EFB′,∴EF∩B′F=F,
∴D′M⊥面EFB′.
点评:本题考查二面角的正切值的求法,考查直线与平面垂直的证明,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
算法的计算规则以及相应的计算步骤必须是唯一确定的,既不能含糊其辞,也不能有多种可能.这里指的是算法的( )
| A、有序性 | B、明确性 |
| C、可行性 | D、不确定性 |
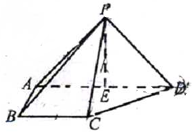 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=