题目内容
若不等式
＜0对?x恒成立，求实数m的取值范围．
| x2-8x+20 |
| mx2-mx-1 |
考点：函数恒成立问题
专题：不等式的解法及应用
分析：给出的分式不等式的分子恒大于0，因此不等式恒成立转化为二次不等式恒成立问题，然后分m=0和m≠0讨论，当m≠0时只需二次项系数小于0，且判别式小于0联立不等式组求解．
解答：
解：∵x2-8x+20=（x-4）2+4＞0，
∴不等式
＜0对?x∈R恒成立可化为：mx2-mx-1＜0对?x∈R恒成立，
当m=0时，mx2-mx-1=-1＜0对?x∈R恒成立；
当m≠0时，要使mx2-mx-1＜0对?x∈R恒成立，
则
，解得-4＜m＜0．
综上，使不等式
＜0对?x∈R恒成立的实数m的取值范围是（-4，0]．
∴不等式
| x2-8x+20 |
| mx2-mx-1 |
当m=0时，mx2-mx-1=-1＜0对?x∈R恒成立；
当m≠0时，要使mx2-mx-1＜0对?x∈R恒成立，
则
|
综上，使不等式
| x2-8x+20 |
| mx2-mx-1 |
点评：本题考查恒成立问题，考查数学转化思想方法和分类讨论的数学思想方法，训练了利用“三个二次”结合求解含参数的最值问题，是中档题．
练习册系列答案
相关题目
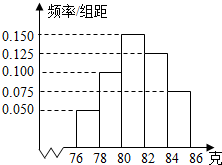某厂对一批产品进行抽样检测，图2是抽检产品净重（单位：克）数据的频率分布直方图，样本数据分组为[76，78）、[78，80）、…、[84，86]．若这批产品有120个，估计其中净重大于或等于78克且小于84克的产品的个数是若
，
是夹角为60°的单位向量，则
=2
+
，
=3
+2
的夹角为（ ）
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
“p∨q是真命题”是“?p为假命题”的（ ）
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
如图，四棱锥P-ABCD中，底面ABCD是菱形，∠ABC=60°，平面PAB⊥平面ABCD，PA=PB=2AB．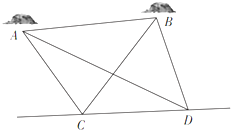
如图，A，B是海平面上的两个小岛，为测量A，B两岛间的距离，测量船以15海里/小时的速度沿既定直线CD航行，在t1时刻航行到C处，测得∠ACB=75°，∠ACD=120°，1小时后，测量船到达D处，测得∠ADC=30°，∠ADB=45°，求A，B两小岛间的距离．（注：A、B、C、D四点共面）
如图，△BCD与△MCD都是边长为2的正三角形，平面MCD⊥平面BCD，AB⊥平面BCD，且AB=
如图，圆锥顶点为P，其母线与底面所成的角为60°，AB过底面圆心O点，且∠CBA=60°．