题目内容

若
e1
，
e2
是夹角为60°的单位向量，则
a
=2
e1
+
e2
，
b
=3
e1
+2
e2
的夹角为（　　）
A、
π
6
B、
π
3
C、
2π
3
D、
5π
6
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由向量的乘法运算及数量积运算求出
a
•
b
，由向量模的公式求出|
a
|，|
b
|，代入两向量夹角公式得答案．
解答： 解：∵
e1
，
e2
是夹角为60°的单位向量，
∴
a
•
b
=(2
e1
+
e2
)•(-3
e1
+2
e2
)
=-6|
e1
|2+
e1
•
e2
+2|
e2
|2=-6+|
e1
|•|
e2
|cos60°+2=-4+1×1×
1
2
=-
7
2
．
|
a
|2=|2
e1
+
e2
|2=4(
e1
)2+4
e1
•
e2
+(
e2
)2
=4+4|
e1
|•|
e2
|cos60°+1=5+4×
1
2
=7．
∴|
a
|=
7
．
|
b
|2=|-3
e1
+2
e2
|2=9|
e1
|2-12
e1
•
e2
+4|
e2
|2
=9-12|
e1
|•|
e2
|cos60°+4=9-12×
1
2
+4=7．
∴|
b
|=
7
．
∴cos＜
a
，
b
＞=
a
•
b
|
a
|•|
b
|
=
-
7
2
7
•
7
=-
1
2
．
∵两向量夹角范围为[0，π]，
∴
a
=2
e1
+
e2
，
b
=3
e1
+2
e2
的夹角为
2π
3
．
故选：C．
点评：本题考查了平面向量的数量积运算，考查了多项式的乘法运算及数量积公式，考查了计算能力，是中档题．
练习册系列答案
相关题目
已知等差数列{an}中，a2=4；a4是a2与a8的等比中项．
（Ⅰ）求数列{an}的通项公式：
（Ⅱ）若an+1≠an．求数列{2n-1an}的前n项和．
在平面直角坐标系中，定义d（P，Q）=|x1-x2|+|y1-y2|为P（x1，y1），Q（x2，y2）两点之间的“折线距离”，则椭圆
x2
2
+y2=1上一点P与直线3x+4y-12=0上一点Q的“折线距离”的最小值为
 
．
已知F1，F2分别是双曲线
x2
a2
-
y2
b2
=1的左、右焦点，过F1的直线l与双曲线的左、右两支分别交于A、B两点．若△ABF2是等边三角形，则该双曲线的离心率为（　　）
A、2
B、
7
C、
13
D、
15
下列说法中错误的是（　　）
A、对于命题p：x0∈R，sin x0＞1，则￢p：x∈R，sin x≤1
B、命题“若0＜a＜1，则函数f（x）=ax在R上是增函数”的逆命题为假命题
C、若p∨q为真命题，则p，q均为真命题
D、命题“若x2-x-2=0，则x=2”的逆否命题是“若x≠2，则x2-x-2≠0”
下列说法：
①命题“若x＞0，则2x＞1”的否命题是“若x≤0，则2x≤1”；
②关于x的不等式a＜sin2x+
1
sin2x
恒成立，则a的取值范围是a＜3；
③函数f（x）=alog2|x|+x+b为奇函数的充要条件是a+b=0；
其中正确的个数是（　　）
A、3B、2C、1D、0
执行如图所示的程序框图．若输入x=7，则输出k的值是（　　）
A、2B、3C、4D、5
若不等式
x2-8x+20
mx2-mx-1
＜0对?x恒成立，求实数m的取值范围．
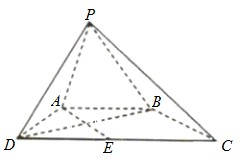如图，在四棱锥P-ABCD中，AB∥CD，△PAB和△PAD是两个边长为2的正三角形．DC=4，PD⊥PB，点E在线段CD上．
（Ⅰ）当
DE
EC
为何值时，AE⊥面PBD：
（Ⅱ）求直线CB与平面PDC所成角的正弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网