题目内容
 如图,四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,平面PAB⊥平面ABCD,PA=PB=2AB.
如图,四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,平面PAB⊥平面ABCD,PA=PB=2AB.(1)证明:PC⊥AB;
(2)求二面角B-PC-D的余弦值.
考点:与二面角有关的立体几何综合题,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(1)由已知条件推导出四边形ABCD是菱形,从而得到CO⊥AB,AB⊥平面POC,由此能够证明AB⊥PC.
(2)由已知条件推导出PO⊥平面ABCD,建立空间直角坐标系O-xyz,利用向量法能求出二面角B-PC-D的余弦值.
(2)由已知条件推导出PO⊥平面ABCD,建立空间直角坐标系O-xyz,利用向量法能求出二面角B-PC-D的余弦值.
解答:
(1)证明:连结AC,设AB的中点为O.连结PO,CO,
∵PA=PB,O是AB的中点,∴PO⊥AB,
∴四边形ABCD是菱形,∠ABC=60°,
∴△ABC是等边三角形,∴CO⊥AB,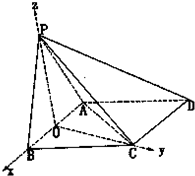
∴AB⊥平面POC,
∵PC?平面POC,∴AB⊥PC.
(2)∵平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,
PO⊥AB,PO?平面ABCD,
∴PO⊥平面ABCD,
建立如图的空间直角坐标系O-xyz,
设AB=2,由(1)得PA=PB=4,PO=
,OC=
,
∴P(0,0,
),B(1,0,0),C(0,
,0),D(-2,
,0),
∴
=(-1,
,0),
=(-2,0,0),
=(0,-
,
),
设平面BCP的一个法向量
=(x,y,z),则
•
=0,
•
=0,
∴
,∴
=(
,
,1),
设平面PCD的一个法向量为
=(x1,y1,z1),则
•
=0,
•
=0,
∴
,∴
=(0,
,1),
∴cos<
,
>=
=
,
∵二面角B-PC-D的平面角是钝角,
∴二面角B-PC-D的余弦值为-
.
∵PA=PB,O是AB的中点,∴PO⊥AB,
∴四边形ABCD是菱形,∠ABC=60°,
∴△ABC是等边三角形,∴CO⊥AB,

∴AB⊥平面POC,
∵PC?平面POC,∴AB⊥PC.
(2)∵平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,
PO⊥AB,PO?平面ABCD,
∴PO⊥平面ABCD,
建立如图的空间直角坐标系O-xyz,
设AB=2,由(1)得PA=PB=4,PO=
| 15 |
| 3 |
∴P(0,0,
| 15 |
| 3 |
| 3 |
∴
| BC |
| 3 |
| CD |
| CP |
| 3 |
| 15 |
设平面BCP的一个法向量
| n |
| n |
| BC |
| n |
| CP |
∴
|
| n |
| 15 |
| 5 |
设平面PCD的一个法向量为
| m |
| m |
| CD |
| m |
| CP |
∴
|
| m |
| 5 |
∴cos<
| m |
| n |
| 5+1 | ||||
|
| ||
| 7 |
∵二面角B-PC-D的平面角是钝角,
∴二面角B-PC-D的余弦值为-
| ||
| 7 |
点评:本题考查异面直线垂直的证明,考查二面角的余弦值的求法,解题时要注意合理地化空间问题为平面问题,注意向量法的合理运用.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
下列说法中错误的是( )
| A、对于命题p:x0∈R,sin x0>1,则¬p:x∈R,sin x≤1 |
| B、命题“若0<a<1,则函数f(x)=ax在R上是增函数”的逆命题为假命题 |
| C、若p∨q为真命题,则p,q均为真命题 |
| D、命题“若x2-x-2=0,则x=2”的逆否命题是“若x≠2,则x2-x-2≠0” |
执行如图所示的程序框图.若输入x=7,则输出k的值是( )


| A、2 | B、3 | C、4 | D、5 |
下列说法正确的是( )
| A、?x0∈R,ex0≤0 | ||
| B、对?a>b,则ab=2,(a2+b2)min=4 | ||
| C、a>1,b>1是ab>1的充分条件 | ||
D、a+b=0的充要条件是
|

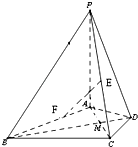 在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°.
在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°.