题目内容
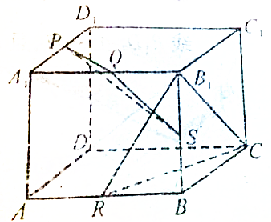 如图,正方体ABCD-A1B1C1D1中,已知Q、P、R、S分别是各棱的中点.求证:平面PQS⊥平面B1RC.
如图,正方体ABCD-A1B1C1D1中,已知Q、P、R、S分别是各棱的中点.求证:平面PQS⊥平面B1RC.考点:平面与平面垂直的判定
专题:空间位置关系与距离
分析:建立空间直角坐标系,先证PS垂直RC,PS垂直B1R得到PS⊥平面 B1RC,再利用面面垂直的判定定理解答.
解答:
证明:分别以BA,BC,BB'为x,y,z轴建立坐标系,设正方体的棱长为2,
则R(1,0,0),C(0,2,0),B1(0,0,2),S(0,0,1),P(2,1,2),
所以
=(-1,2,0),
=(0,2,-2),
=(2,1,1),
因为
•
=-2+2+0=0,
•
=0+2-2=0,
所以RC⊥PS,B1C⊥PS,
所以PS⊥平面B1RC,
PS?平面PSQ,
所以平面PQS⊥平面B1RC.
则R(1,0,0),C(0,2,0),B1(0,0,2),S(0,0,1),P(2,1,2),
所以
| RC |
| B1C |
| PS |
因为
| RC |
| PS |
| B1C |
| PS |
所以RC⊥PS,B1C⊥PS,
所以PS⊥平面B1RC,
PS?平面PSQ,
所以平面PQS⊥平面B1RC.
点评:本题考查了正方体为载体的面面垂直的判断;关键是将面面垂直转化为线面垂直和线线垂直,体现了转化的思想.

练习册系列答案
相关题目
直线kx-y+3k-2=0恒过一定点,则该定点的坐标( )
| A、(3,2) |
| B、(-3,-2) |
| C、(2,3) |
| D、(-2,-3) |
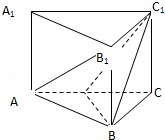 已知正三棱柱ABC-A1B1C1的底面边长为8,侧棱长为6,D为AC中点.
已知正三棱柱ABC-A1B1C1的底面边长为8,侧棱长为6,D为AC中点. 如图,P为平行四边形ABCD所在平面外一点,平面PAD∩平面PBC=m.求证:BC∥m.
如图,P为平行四边形ABCD所在平面外一点,平面PAD∩平面PBC=m.求证:BC∥m.