题目内容
南宁市十二路公共汽车每5分钟一趟,某位同学每天乘十二路公共汽车上学,则他等车时间小于3分钟的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:计算题,概率与统计
分析:由题意知本题是一个几何概型,试验包含的所有事件是汽车5分钟一班准时到达车站.而满足条件的事件是任一人在该车站等车时间少于3分钟,根据几何概型概率公式得到结果.
解答:
解:由题意知本题是一个几何概型,
试验包含的所有事件是汽车5分钟一班准时到达车站,时间长度是5,
而满足条件的事件是任一人在该车站等车时间少于3分钟的时间长度是3,
由几何概型概率公式得到P=
,
故选:B.
试验包含的所有事件是汽车5分钟一班准时到达车站,时间长度是5,
而满足条件的事件是任一人在该车站等车时间少于3分钟的时间长度是3,
由几何概型概率公式得到P=
| 3 |
| 5 |
故选:B.
点评:本题考查几何概型,几何概型的概率的值是通过长度、面积、和体积、的比值得到.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
设函数f(x)=x2-12x+b,则下列结论正确的是( )
| A、函数f(x)在(-∞,-1)上单调递增 |
| B、函数f(x)在(-∞,-1)上单调递减 |
| C、若b=-6,则函数f(x)的图象在点(-2,f(-2))处的切线方程为y=10 |
| D、若b=0,则函数f(x)的图象与直线y=10只有一个公共点 |
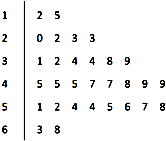 对某商店一个月30天内每天的顾客人数进行了统计,得到样本的茎叶图(如图所示),则该样本的中位数、众数、极差分别是( )
对某商店一个月30天内每天的顾客人数进行了统计,得到样本的茎叶图(如图所示),则该样本的中位数、众数、极差分别是( )| A、46,45,56 |
| B、46,45,53 |
| C、47,45,56 |
| D、45,47,53 |
若AD为△ABC的中线,现有质地均匀的粒子散落在△ABC内,则粒子在△ABD内的概率等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
两条直线x+2y+1=0与2x-y+1=0的位置关系是( )
| A、平行 | B、垂直 |
| C、相交且不垂直 | D、重合 |
已知函数f(x)=sin(
-x)(x∈R),下面结论正确的是( )
| π |
| 2 |
A、函数f(x)的最小正周期为
| ||
B、函数f(x)在区间[0,
| ||
| C、函数f(x)是奇函数 | ||
| D、函数f(x)的图象关于直线x=0对称 |
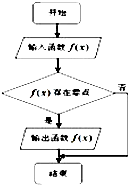 执行如图所示的程序框图,若输入如下四个函数:
执行如图所示的程序框图,若输入如下四个函数: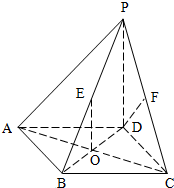 已知在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧棱PD⊥平面ABCD,且PD=2,O为底面对角线的交点,E、F分别为棱PB,PC的中点
已知在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧棱PD⊥平面ABCD,且PD=2,O为底面对角线的交点,E、F分别为棱PB,PC的中点