题目内容
定义集合A、B之间的运算如下:A-B=A∩∁∪B,A⊙B=(A-B)∪(B-A),已知U={x|x≤9,x∈N},X={0,2,4,6,8},Y={1,2,4,8},则X-Y= ;X⊙Y= ;若(Z-X)⊆(Y-X),则满足条件的集合Z有 个.
考点:交、并、补集的混合运算
专题:集合
分析:根据题意的新定义求出出X-Y,X⊙Y,确定出Z即可.
解答:
解:∵U={x|x≤9,x∈N}={0,1,2,3,4,5,6,7,8,9},X={0,2,4,6,8},Y={1,2,4,8},
∴∁UY={0,3,5,6,7,9},∁UX={1,3,5,7,9},
∴X-Y=X∩∁UY={0,6};Y-X=Y∩∁UX={1},
∴X⊙Y=(X-Y)∪(Y-X)={0,1,6},
∵Y-X=Y∩∁UX={1};Z-X=Z∩∁UX,
∵(Z-X)⊆(Y-X),
∴Z={1}.
故答案为:{0,6};{0,1,6};1
∴∁UY={0,3,5,6,7,9},∁UX={1,3,5,7,9},
∴X-Y=X∩∁UY={0,6};Y-X=Y∩∁UX={1},
∴X⊙Y=(X-Y)∪(Y-X)={0,1,6},
∵Y-X=Y∩∁UX={1};Z-X=Z∩∁UX,
∵(Z-X)⊆(Y-X),
∴Z={1}.
故答案为:{0,6};{0,1,6};1
点评:此题考查了交、并、补集的混合运算,弄清题中的新定义是解本题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
在如图以O为中心的正六边形上随机投一粒黄豆,则这粒黄豆落到阴影部分的概率为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
设函数f(x)=x2-12x+b,则下列结论正确的是( )
| A、函数f(x)在(-∞,-1)上单调递增 |
| B、函数f(x)在(-∞,-1)上单调递减 |
| C、若b=-6,则函数f(x)的图象在点(-2,f(-2))处的切线方程为y=10 |
| D、若b=0,则函数f(x)的图象与直线y=10只有一个公共点 |
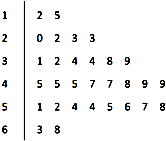 对某商店一个月30天内每天的顾客人数进行了统计,得到样本的茎叶图(如图所示),则该样本的中位数、众数、极差分别是( )
对某商店一个月30天内每天的顾客人数进行了统计,得到样本的茎叶图(如图所示),则该样本的中位数、众数、极差分别是( )| A、46,45,56 |
| B、46,45,53 |
| C、47,45,56 |
| D、45,47,53 |
已知函数f(x)=sin(
-x)(x∈R),下面结论正确的是( )
| π |
| 2 |
A、函数f(x)的最小正周期为
| ||
B、函数f(x)在区间[0,
| ||
| C、函数f(x)是奇函数 | ||
| D、函数f(x)的图象关于直线x=0对称 |