题目内容
△ABC的内角A、B、C所对的边分别为a,b,c,若三边的长为连续的三个正整数,且A>B>C,9b=10acosC,则sinA:sinB:sinC为( )
| A、4:3:2 |
| B、5:6:7 |
| C、5:4:3 |
| D、6:5:4 |
考点:正弦定理
专题:解三角形
分析:根据题意分别用c表示出a和b,利用已知等式和余弦定理建立方程求得c,则a和b可得.
解答:
解:∵因为a,b,c为连续的三个正整数,且A>B>C,可得a>b>c,所以a=c+2,b=c+1①;
又因为已知9b=10acosC,所以cosC=
②.由余弦定理可得cosC=
③,则由②③可得
=
④,联立①④,得c2-3c-4=0,
求得c=4或-1(舍去),
∴a=6,b=5,
∴sinA:sinB:sinC=a:b:c=6:5:4,
故选:D.
又因为已知9b=10acosC,所以cosC=
| 9b |
| 10a |
| a2+b2-c2 |
| 2ab |
| 9b |
| 10a |
| a2+b2-c2 |
| 2ab |
求得c=4或-1(舍去),
∴a=6,b=5,
∴sinA:sinB:sinC=a:b:c=6:5:4,
故选:D.
点评:本题考查正、余弦定理以及三角形中大角对大边的应用.本题最终需求解三个角的正弦的比值,明显是要利用正弦定理转化为边长的比值,因此必须求出三边长.

练习册系列答案
相关题目
设函数f(x)=x2-12x+b,则下列结论正确的是( )
| A、函数f(x)在(-∞,-1)上单调递增 |
| B、函数f(x)在(-∞,-1)上单调递减 |
| C、若b=-6,则函数f(x)的图象在点(-2,f(-2))处的切线方程为y=10 |
| D、若b=0,则函数f(x)的图象与直线y=10只有一个公共点 |
下列说法正确的是( )
A、甲掷硬币10次,正面向上3次,则正面向上的概率为
| ||
B、某种彩票中奖的概率为
| ||
C、某地天气预报说明天下雨的概率是
| ||
D、掷一颗骰子一次得到3向上的概率为
|
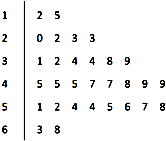 对某商店一个月30天内每天的顾客人数进行了统计,得到样本的茎叶图(如图所示),则该样本的中位数、众数、极差分别是( )
对某商店一个月30天内每天的顾客人数进行了统计,得到样本的茎叶图(如图所示),则该样本的中位数、众数、极差分别是( )| A、46,45,56 |
| B、46,45,53 |
| C、47,45,56 |
| D、45,47,53 |
两条直线x+2y+1=0与2x-y+1=0的位置关系是( )
| A、平行 | B、垂直 |
| C、相交且不垂直 | D、重合 |
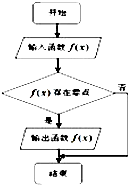 执行如图所示的程序框图,若输入如下四个函数:
执行如图所示的程序框图,若输入如下四个函数: