题目内容
已知函数f(x)=x2+bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2014的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:数列的求和
专题:等差数列与等比数列
分析:利用导数的几何意义赇 出f(x)=x2+x,从而得到an=
=
=
-
,由此利用裂项求和法能求出S2014.
| 1 |
| f(n) |
| 1 |
| n2+n |
| 1 |
| n |
| 1 |
| n+1 |
解答:
解:∵f(x)=x2+bx,∴f′(x)=2x+b
∵直线3x-y+2=0的斜率为k=3,
函数f(x)=x2+bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,
∴f′(1)=2+b=3,解得b=1,
∴f(x)=x2+x,
∴an=
=
=
-
,
∴Sn=(1-
)+(
-
)+…+(
-
)=1-
=
,
∴S2014=
.
故选:B.
∵直线3x-y+2=0的斜率为k=3,
函数f(x)=x2+bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,
∴f′(1)=2+b=3,解得b=1,
∴f(x)=x2+x,
∴an=
| 1 |
| f(n) |
| 1 |
| n2+n |
| 1 |
| n |
| 1 |
| n+1 |
∴Sn=(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
| n |
| n+1 |
∴S2014=
| 2014 |
| 2015 |
故选:B.
点评:本题考查数列的前2014项的和的求法,是中档题,解题时要认真审题,注意导数的几何意义和裂项求和法的合理运用.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
双曲线
-
=1的焦点到渐近线的距离与顶点到渐近线的距离之比为( )
| x2 |
| 4 |
| y2 |
| 5 |
A、
| ||
B、
| ||
| C、2 | ||
D、
|
学校为了了解高二年级教学情况,对清北班、重点班、普通班、艺术班的学生做分层抽 样调查,假设学校高二年级总人数为N,其中清北班有学生144人,若在清北班、重点班、普通班、艺术班抽取的人数分别为18,66,53,24,则总人数N为( )
| A、801 | B、1 288 |
| C、853 | D、912 |
函数f(x)=cos(
-x)cosx是( )
| π |
| 2 |
| A、最小正周期为π的奇函数 | ||
B、最小正周期为
| ||
| C、最小正周期为π的偶函数 | ||
D、最小正周期为
|
方程x-1=
表示的曲线是( )
| 1-(y-1)2 |
| A、一个圆 | B、两个半圆 |
| C、两个圆 | D、半圆 |
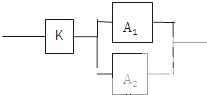 如图.用K,A1,A2分别不同的原件连接成一个系统.当K正常工作且A1和A2正常工作的概率是0.9,0.8,0.8则系统正常工作的概率为( )
如图.用K,A1,A2分别不同的原件连接成一个系统.当K正常工作且A1和A2正常工作的概率是0.9,0.8,0.8则系统正常工作的概率为( )| A、0.960 | B、0.864 |
| C、0.72 | D、0.576 |
已知向量
=(-
,
),且向量
在向量
的方向上的投影为
,则
•
为( )
| a |
| 12 |
| 13 |
| 5 |
| 13 |
| b |
| a |
| 13 |
| a |
| b |
A、
| ||
B、
| ||
| C、13 | ||
D、
|