题目内容
已知随机变量X+Y=8，如果X～N（10，0.6），则E（Y）、D（Y）分别是多少？
考点：正态分布曲线的特点及曲线所表示的意义
专题：概率与统计
分析：本题考查正态分布的相关知识．先由X～N（10，0.6），得均值E（X）=10，方差D（X）=0.6，然后由X+Y=8得Y=-X+8，再根据公式求解即可．
解答：
解：由题意X～N（10，0.6），知随机变量X服从均值E（X）=10，方差D（X）=0.6的正态分布，
又∵X+Y=8，
∴Y=-X+8，
∴E（Y）=-E（X）+8=-10+8=-2，D（Y）=（-1）2D（X）=0.6．
又∵X+Y=8，
∴Y=-X+8，
∴E（Y）=-E（X）+8=-10+8=-2，D（Y）=（-1）2D（X）=0.6．
点评：解题关键是：若两个随机变量Y，X满足一次关系式Y=aX+b（a，b为常数），当已知E（X）、D（X）时，则有E（Y）=aE（X）+b，D（Y）=a2D（X）．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
已知全集U=R，A={x|x＞1}，B={x|x2-2x＞0}，则∁U（A∪B）=（ ）
| A、{x|x≤2} |
| B、{x|x≥1} |
| C、{x|0≤x≤1} |
| D、{x|0≤x≤2} |
函数y=ln（x-2）的定义域是（ ）
| A、（-∞，+∞） |
| B、（-∞，2） |
| C、（0，2） |
| D、（2，+∞） |
在正方体ABCD-A1B1C1D1中，E，F分别为A1D1，CC1的中点，P为A1B1上的一动点，则PF与AE所成的角为（ ）
| A、45° | B、60° |
| C、90° | D、不确定 |
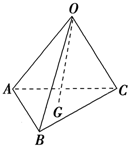如图，在三棱锥O-ABC中，G是△ABC的重心，若| OA |
| a |
| OB |
| b |
| OC |
| c |
| a |
| b |
| c |
| OG |
A、
| ||||||
B、
| ||||||
| C、a+b+c | ||||||
| D、3a+3b+3c |