题目内容
已知指数函数y=g(x)满足:g(2)=4,定义域为R的函数f(x)=
是奇函数.
(1)求a,b的值;
(2)判断函数f(x)的单调性并用定义加以证明;
(3)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求实数k的取值范围.
| -g(x)+a |
| 2g(x)+b |
(1)求a,b的值;
(2)判断函数f(x)的单调性并用定义加以证明;
(3)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求实数k的取值范围.
考点:函数单调性的判断与证明,函数单调性的性质
专题:函数的性质及应用,不等式的解法及应用
分析:本题(1)利用直线过定点和函数为奇函数,得到关于参数的方程组,解方程组得到本题结论;(2)利用函数单调性的定义加以证明,得到本题结论;(3)利用函数的奇偶性和单调性,将原不等式转化为相应自变量的比较,解不等式得到本题结论.
解答:
解:(1)设g(x)=mx(m>0,m≠1)
∵g(2)=4,
∴m2=4,
∴m=2,
∴g(x)=2x.
∴f(x)=
,
∵定义域为R的函数f(x)=
是奇函数,
∴
,
∴
.
(2)函数f(x)是R上的减函数,下面证明.
证明:由(1)可知:f(x)=
=-
+
,
任取x1,x2∈R,且x1<x2,
则:f(x1)-f(x2)=(-
+
)-(-
+
)=
,
∵x1<x2,
∴2 x2>2x1,2x1+1>0,2x2+1>0,
∴f(x1)-f(x2)>0,
∴f(x1)>f(x2).
∴函数f(x)是R是上的单调递减函数.
(3)∵f(2t2-2t)+f(2t2-k)<0对于任意的t∈R恒成立,
∴f(t2-2t)<-f(2t2-k).
∵定义域为R的函数f(x)是奇函数,
∴f(t2-2t)<f(k-2t2).
∵函数f(x)是R上的减函数,
∴t2-2t>k-2t2,
∴k<3t2-2t=2(t-
)2-
对于任意的t∈R恒成立,
∴k<-
.
∵g(2)=4,
∴m2=4,
∴m=2,
∴g(x)=2x.
∴f(x)=
| -2x+a |
| 2•2x+b |
∵定义域为R的函数f(x)=
| -g(x)+a |
| 2g(x)+b |
∴
|
∴
|
(2)函数f(x)是R上的减函数,下面证明.
证明:由(1)可知:f(x)=
| -2x+1 |
| 2•2x+2 |
| 1 |
| 2 |
| 1 |
| 2x+1 |
任取x1,x2∈R,且x1<x2,
则:f(x1)-f(x2)=(-
| 1 |
| 2 |
| 1 |
| 2x1+1 |
| 1 |
| 2 |
| 1 |
| 2x2+1 |
| 2x2-2x1 |
| (2x1+1)(2x2+1) |
∵x1<x2,
∴2 x2>2x1,2x1+1>0,2x2+1>0,
∴f(x1)-f(x2)>0,
∴f(x1)>f(x2).
∴函数f(x)是R是上的单调递减函数.
(3)∵f(2t2-2t)+f(2t2-k)<0对于任意的t∈R恒成立,
∴f(t2-2t)<-f(2t2-k).
∵定义域为R的函数f(x)是奇函数,
∴f(t2-2t)<f(k-2t2).
∵函数f(x)是R上的减函数,
∴t2-2t>k-2t2,
∴k<3t2-2t=2(t-
| 1 |
| 3 |
| 1 |
| 3 |
∴k<-
| 1 |
| 3 |
点评:本题考查了函数的奇偶性和单调性,本题难度适中,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
将长为1的小棒随机拆成3小段,则这3小段能构成三角形的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=
ln(1-x)的定义域为( )
| x+1 |
| A、[-1,1) |
| B、(-1,1) |
| C、(-1,1] |
| D、[-1,1] |
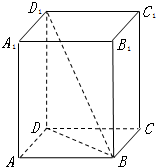 如图,长方体ABCD-A1B1C1D1中,ABCD是边长为1的正方形,D1B=
如图,长方体ABCD-A1B1C1D1中,ABCD是边长为1的正方形,D1B=