题目内容
如果函数f(x)=x2+bx+c对任意实数均有f(-x)=f(x),那么( )
| A、f(-2)<f(1)<f(3) |
| B、f(3)<f(-2)<f(1) |
| C、f(-2)<f(3)<f(1) |
| D、f(1)<f(-2)<f(3) |
考点:二次函数的性质
专题:计算题,函数的性质及应用
分析:由条件可知f(x)为偶函数,b=0,从而得到当x>0时,f(x)是单调递增,则f(-2)=f(2),由单调性,即可判断大小.
解答:
解:∵函数f(x)=x2+bx+c对任意实数均有f(-x)=f(x),
∴f(x)为偶函数,b=0,
∴f(-2)=f(2),
当x>0时,f(x)是单调递增,
∵1<2<3,∴f(1)<f(2)<f(3),
即f(1)<f(-2)<f(3),
故选D.
∴f(x)为偶函数,b=0,
∴f(-2)=f(2),
当x>0时,f(x)是单调递增,
∵1<2<3,∴f(1)<f(2)<f(3),
即f(1)<f(-2)<f(3),
故选D.
点评:本题考查函数的奇偶性、单调性及其运用,注意定义的运用是正确解题的关键,本题属于基础题.

练习册系列答案
相关题目
函数y=|sinx|(-
<x<
)的大致图象是( )
| π |
| 2 |
| π |
| 2 |
A、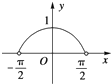 |
B、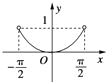 |
C、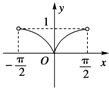 |
D、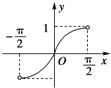 |
函数f(x)=log0.5(x2-2x+3)的单调递减区间是( )
| A、(1,2) |
| B、[1,+∞) |
| C、(0,+∞) |
| D、(-∞,1] |
函数f(x)=1-lnx的零点所在的区间是( )
| A、(1,2) |
| B、(2,3) |
| C、(3,4) |
| D、(4,5) |
已知sinα=
,则cosα=( )
| 1 |
| 3 |
A、
| ||||||||
B、-
| ||||||||
C、
| ||||||||
D、
|
数列1
,2
,3
,4
…前n项的和为( )
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、-
|