题目内容
正方体上的点P、Q、R、S是其所在棱的中点,则直线PQ与直线RS异面的图形是( )
A、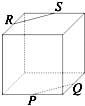 |
B、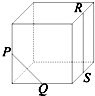 |
C、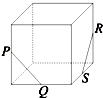 |
D、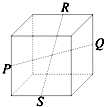 |
考点:异面直线的判定
专题:空间位置关系与距离
分析:(1)分析:A 根据正方体上的点P、Q、R、S是其所在棱的中点,则知RS平行于上底面一条对角线的连线,进一步确定RS∥PQ,故PQ和RS不是异面直线.
(2)分析:C 根据正方体上的点P、Q、R、S是其所在棱的中点,延长PQ,RS以及外右侧的棱然后根据三角形的相似得PQ和RS是相交直线.
(3)分析:D 根据正方体上的点P、Q、R、S是其所在棱的中点,连接PS和RQ,利用平行公理得到PS∥RQ,说明P、S、R、Q四点共面,进一步得到:PQ和RS是相交直线.
(2)分析:C 根据正方体上的点P、Q、R、S是其所在棱的中点,延长PQ,RS以及外右侧的棱然后根据三角形的相似得PQ和RS是相交直线.
(3)分析:D 根据正方体上的点P、Q、R、S是其所在棱的中点,连接PS和RQ,利用平行公理得到PS∥RQ,说明P、S、R、Q四点共面,进一步得到:PQ和RS是相交直线.
解答:
解:(1)分析:A 根据正方体上的点P、Q、R、S是其所在棱的中点,则知RS平行于上底面一条对角线的连线,进一步确定RS∥PQ,故PQ和RS不是异面直线.
(2)分析:C 根据正方体上的点P、Q、R、S是其所在棱的中点,延长PQ,RS以及外右侧的棱然后根据三角形的相似得PQ和RS是相交直线.
(3)分析:D 根据正方体上的点P、Q、R、S是其所在棱的中点,连接PS和RQ,利用平行公理得到PS∥RQ,说明P、S、R、Q四点共面,进一步得到:PQ和RS是相交直线.
通过排除法
故选:B
(2)分析:C 根据正方体上的点P、Q、R、S是其所在棱的中点,延长PQ,RS以及外右侧的棱然后根据三角形的相似得PQ和RS是相交直线.
(3)分析:D 根据正方体上的点P、Q、R、S是其所在棱的中点,连接PS和RQ,利用平行公理得到PS∥RQ,说明P、S、R、Q四点共面,进一步得到:PQ和RS是相交直线.
通过排除法
故选:B
点评:本题考查的知识点:异面直线的判定方法,即否定(1)在同一平面内(2)否定平行(3)否定相交.

练习册系列答案
相关题目
某简单几何体的三视图如图所示,则该几何体为( )


| A、圆柱 | B、圆锥 | C、圆台 | D、棱锥 |
 如图,圆内接四边形ABCD中,AD∥BC,AC与BD交于点E,在图中全等三角形的对数为( )
如图,圆内接四边形ABCD中,AD∥BC,AC与BD交于点E,在图中全等三角形的对数为( )| A、2对 | B、3对 | C、4对 | D、5对 |
如果函数f(x)=x2+bx+c对任意实数均有f(-x)=f(x),那么( )
| A、f(-2)<f(1)<f(3) |
| B、f(3)<f(-2)<f(1) |
| C、f(-2)<f(3)<f(1) |
| D、f(1)<f(-2)<f(3) |
如果奇函数f(x)在区间[2,6]上是增函数,且最小值为4,则f(x)在[-6,-2]上是( )
| A、最大值为-4的增函数 |
| B、最小值为-4的增函数 |
| C、最小值为-4的减函数 |
| D、最大值为-4的减函数 |
某校有高一学生300人,高二学生270人,高三学生210人,现教育局督导组欲用分层抽样的方法抽取26名学生进行问卷调查,则下列判断正确的是( )
| A、高一学生被抽到的概率最大 |
| B、高三学生被抽到的概率最大 |
| C、高三学生被抽到的概率最小 |
| D、每名学生被抽到的概率相等 |