题目内容
已知△ABC中，a=b=4，c=4
，则∠C=（ ）
| 3 |
| A、150° |
| B、30°或150° |
| C、120° |
| D、60°或120° |
考点：余弦定理
专题：解三角形
分析：利用余弦定理列出关系式，将a，b，c的值代入计算求出cosC的值，即可确定出C的度数．
解答：
解：∵在△ABC中，a=b=4，c=4
，
∴cosC=
=
=-
，
则∠C=120°．
故选：C．
| 3 |
∴cosC=
| a2+b2-c2 |
| 2ab |
| 16+16-48 |
| 32 |
| 1 |
| 2 |
则∠C=120°．
故选：C．
点评：此题考查了余弦定理，以及特殊角的三角函数值，熟练掌握余弦定理是解本题的关键．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
由曲线y2=x与y=x，y=
所围成图形的面积是（ ）
| 3 |
A、S=
| ||||||
B、S=
| ||||||
C、S=
| ||||||
D、S=
|
已知双曲线
-y2=1（a＞0）的实轴长为2，则该双曲线的离心率为（ ）
| x2 |
| a2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知x＞0，n∈N*，由下列结论x+
≥2，x+
≥3，x+
≥4，…，得到一个正确的结论可以是（ ）
| 1 |
| x |
| 4 |
| x2 |
| 27 |
| x3 |
A、x+
| ||
B、x+
| ||
C、x+
| ||
D、x+
|
若双曲线x2-
=1（b＞0）的一条渐近线与圆x2+（y-2）2=1至多有一个交点，则双曲线离心率的取值范围是（ ）
| y2 |
| b2 |
| A、（1，2] | ||
| B、[2，+∞） | ||
C、（1，
| ||
D、[
|
已知f（x）=π（x∈R），则f（π2）=（ ）
| A、π2 | ||
| B、π | ||
C、
| ||
| D、不确定 |
若关于x的不等式x2-x+a＞0恒成立，则a的取值范围为（ ）
A、[
| ||
B、（
| ||
C、（-∞，
| ||
D、（-∞，
|
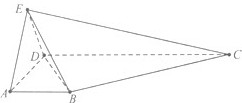如图所示，在四棱锥E-ABCD中，AB∥CD，∠ADC=90°，CD=3，AB=1，EA=AD=DE=2，EC=