题目内容
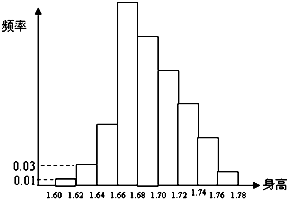 为了解某校身高在1.60m~1.78m的高一学生的情况,随机地抽查了该校100名高一学生,得到如图所示频率直方图.由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为m,身高在1.66m~1.74m的学生数为n,则m,n的值分别为( )
为了解某校身高在1.60m~1.78m的高一学生的情况,随机地抽查了该校100名高一学生,得到如图所示频率直方图.由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为m,身高在1.66m~1.74m的学生数为n,则m,n的值分别为( )| A、0.27,78 |
| B、0.27,83 |
| C、0.81,78 |
| D、0.09,83 |
考点:频率分布直方图
专题:概率与统计
分析:先根据直方图求出前2组的频数,根据前4组成等比数列求出第3和第4组的人数,从而求出后6组的人数,由此能求出结果.
解答:
解:由题意知:
身高在(1.60,1.62]的学生人数为100×0.01=1人,
身高在(1.62,1.64]的学生人数为100×0.03=3人,
身高在(1.64,1.66]的学生人数为3×3=9人,
身高在(1.66,1.68]的学生人数为9×3=27人,
后6组的频数成等差数列,则这个等差数列的首项为27,设公差为d,
则6×27+15d=87,解得d=-5,
∴身高在(1.68,1.70]的学生人数为27-5=22人,
身高在(1.70,1.72]的学生人数为22-5=17人,
身高在(1.72,1.74]的学生人数为17-5=12人,
∴m=
=0.27,
n=27+22+17+12=78.
故选A.
身高在(1.60,1.62]的学生人数为100×0.01=1人,
身高在(1.62,1.64]的学生人数为100×0.03=3人,
身高在(1.64,1.66]的学生人数为3×3=9人,
身高在(1.66,1.68]的学生人数为9×3=27人,
后6组的频数成等差数列,则这个等差数列的首项为27,设公差为d,
则6×27+15d=87,解得d=-5,
∴身高在(1.68,1.70]的学生人数为27-5=22人,
身高在(1.70,1.72]的学生人数为22-5=17人,
身高在(1.72,1.74]的学生人数为17-5=12人,
∴m=
| 27 |
| 100 |
n=27+22+17+12=78.
故选A.
点评:本题考查了频率分布直方图及应用,考查等差数列、等比数列,综合性强.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
在某次数学测验中,记座号为n(n=1,2,3,4)的同学成绩为f(n),若f(n)∈{70,85,88,90,98,100},且满足f(1)<f(2)≤f(3)<f(4),则这四位同学考试成绩的所有可能有( )种.
| A、15 | B、20 | C、30 | D、35 |
设a=0.9-0.9,b=9-0.9,c=log90.9,则( )
| A、a>b>c |
| B、b>a>c |
| C、a>c>b |
| D、c>a>b |
如图所示,甲 乙 丙是三个立体图形的三视图,则甲乙丙对应的标号正确的是( )

| A、④③② | B、②①③ |
| C、①②③ | D、③②④ |
由曲线y2=x与y=x,y=
所围成图形的面积是( )
| 3 |
A、S=
| ||||||
B、S=
| ||||||
C、S=
| ||||||
D、S=
|
已知数列{an},a1=1,a2=4,且an+2=an+1-an,则数列的第6项为( )
| A、-1 | B、-3 | C、3 | D、-4 |
已知x>0,n∈N*,由下列结论x+
≥2,x+
≥3,x+
≥4,…,得到一个正确的结论可以是( )
| 1 |
| x |
| 4 |
| x2 |
| 27 |
| x3 |
A、x+
| ||
B、x+
| ||
C、x+
| ||
D、x+
|
 如图,在等腰梯形ABCD中,AB∥CD,且AB=2CD,设∠DAB=θ,θ∈(0,
如图,在等腰梯形ABCD中,AB∥CD,且AB=2CD,设∠DAB=θ,θ∈(0,