题目内容
甲、乙两人玩抛掷正四面体玩具游戏,现由两枚大小相同,质地均匀的正四面体玩具,每枚玩具的各个面上分别写着数字3,4,5,7,甲先掷一枚玩具,朝下的面上的数字记 为a,乙后掷一枚玩具,朝下的面的数字记为b.
(1)求事件“a+b≥10”的概率;
(2)若游戏规定:当“a+b为奇数”时,甲 赢;当“a+b为偶数时”,乙赢,试问这个规定公平吗?请说明理由.
(1)求事件“a+b≥10”的概率;
(2)若游戏规定:当“a+b为奇数”时,甲 赢;当“a+b为偶数时”,乙赢,试问这个规定公平吗?请说明理由.
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:(1)根据题意,列出玩具出现各面朝下的可能情况有哪些,奇数事件a+b≥10的概率;
(2)计算“a+b为奇数”的概率与“a+b为偶数”的概率,判断这个规定是否公平.
(2)计算“a+b为奇数”的概率与“a+b为偶数”的概率,判断这个规定是否公平.
解答:
解:根据题意,因玩具是均匀的,玩具各面朝下的可能性相等,出现的可能情况有:
(3,3),(3,4),(3,5),(3,7),(4,3),(4,4),(4,5),(4,7),
(5,3),(5,4),(5,5),(5,7),(7,3),(7,4),(7,5),(7,7)共16;
(1)事件“”包含其中的(3,7),(4,7),(5,5),(5,7),(7,3),
(7,4),(7,5),(7,7)共8个基本事件;
∴P(a+b≥10)=
=
;
(2)这个规定不公平,理由是:
∵“a+b为奇数”的概率为
P(a+b=7)+P(a+b=9)+P(a+b=11)=
+
+
=
∴“a+b为偶数”的概率为P=1-
=
,
这两个概率值不相等;
∴这个规定不公平.
(3,3),(3,4),(3,5),(3,7),(4,3),(4,4),(4,5),(4,7),
(5,3),(5,4),(5,5),(5,7),(7,3),(7,4),(7,5),(7,7)共16;
(1)事件“”包含其中的(3,7),(4,7),(5,5),(5,7),(7,3),
(7,4),(7,5),(7,7)共8个基本事件;
∴P(a+b≥10)=
| 8 |
| 16 |
| 1 |
| 2 |
(2)这个规定不公平,理由是:
∵“a+b为奇数”的概率为
P(a+b=7)+P(a+b=9)+P(a+b=11)=
| 2 |
| 16 |
| 2 |
| 16 |
| 2 |
| 16 |
| 3 |
| 8 |
∴“a+b为偶数”的概率为P=1-
| 3 |
| 8 |
| 5 |
| 8 |
这两个概率值不相等;
∴这个规定不公平.
点评:本题考查了古典概型的应用问题,解题时应用列举法计算基本事件数,是基础题.

练习册系列答案
相关题目
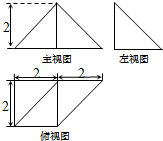
如图所示是一个四棱锥的三视图,则该几何体的体积为( )

| A、4 | ||||
B、
| ||||
| C、12 | ||||
D、
|
在△ABC中,点D在BC边上,且
=2
,
=r
+s
,则r+s=( )
| CD |
| DB |
| CD |
| AB |
| AC |
A、
| ||
B、
| ||
| C、1 | ||
| D、0 |
已知函数f(x)=sin(
x+θ)-
cos(
x+θ)(|θ|<
)的图象关于y中对称,则y=f(x)在下列哪个区间上是减函数( )
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| π |
| 2 |
A、(0,
| ||||
B、(
| ||||
C、(-
| ||||
D、(
|
 如图,海上有A,B两个小岛相距10km,船O将保持观望A岛和B岛所成的视角为60°,现从船O上派下一只小艇沿BO方向驶至C处进行作业,且OC=BO.设AC=xkm.
如图,海上有A,B两个小岛相距10km,船O将保持观望A岛和B岛所成的视角为60°,现从船O上派下一只小艇沿BO方向驶至C处进行作业,且OC=BO.设AC=xkm.