题目内容
PM2.5即细颗粒物是指直径在2.5微米以下的颗粒物,能长时间的悬浮在空气中.PM2.5在空气中的含量越高,代表空气污染越严重.PM2.5的浓度值以每立方米的微克值来表示,我国规定空气中PM2.5的浓度小于或等于75微克/立方米为达标.某市连续监测了一天中0~12时内PM2.5含量的变化情况,其浓度W(t)(微克/立方米)随时刻t的变化可近似表示如下:W(t)=
(1)设k=1,求这一天中0~12时内哪些时间段是达标的?
(2)已知k>0,如果当t∈(6,12]时,PM2.5的浓度始终大于75微克/立方米,求k的取值范围.
|
(1)设k=1,求这一天中0~12时内哪些时间段是达标的?
(2)已知k>0,如果当t∈(6,12]时,PM2.5的浓度始终大于75微克/立方米,求k的取值范围.
考点:基本不等式在最值问题中的应用
专题:应用题,不等式的解法及应用
分析:(1)根据题意得出x∈[0,6],g(x)=x2-x+ln(x+1)+75,利用导数求解.
(2)题意g(x)=kx2-x+ln(x+1)+75>75,?x∈[0,6]成立,利用导数求解,得出:当
≤0即k≥
时,g(x)在(0,6]单调递增,则g(x)>75,
即得出
>0即k<
时成立.
(2)题意g(x)=kx2-x+ln(x+1)+75>75,?x∈[0,6]成立,利用导数求解,得出:当
| 1-2k |
| 2k |
| 1 |
| 2 |
即得出
| 1-2k |
| 2k |
| 1 |
| 2 |
解答:
解:(1)当t∈[0,6)时,令
(t-4)2+65≤75得2≤t<6
当t∈[6,12]时,令t-6=x,则x∈[0,6],g(x)=x2-x+ln(x+1)+75,
g′(x)=2x-1+
=
>0
因此,当g(x)在[0,6]上单调递增,∴g(x)≥g(0)=75
故当2≤t≤6时,PM2.5的浓度达标
(2)由(1)及题意g(x)=kx2-x+ln(x+1)+75>75,?x∈[0,6]成立
g′(x)=2kx-1+
=
所以k≥
符合要求
当
>0即k<
时,g(x)在(0,
)单调递减,
则存在x∈(0,6]使g(x)<g(0)=75,所以k<
不符合要求
综上可知k≥
.
| 5 |
| 2 |
当t∈[6,12]时,令t-6=x,则x∈[0,6],g(x)=x2-x+ln(x+1)+75,
g′(x)=2x-1+
| 1 |
| x+1 |
| 2x2+x |
| x+1 |
因此,当g(x)在[0,6]上单调递增,∴g(x)≥g(0)=75
故当2≤t≤6时,PM2.5的浓度达标
(2)由(1)及题意g(x)=kx2-x+ln(x+1)+75>75,?x∈[0,6]成立
g′(x)=2kx-1+
| 1 |
| x+1 |
2kx(x-
| ||
| x+1 |
所以k≥
| 1 |
| 2 |
当
| 1-2k |
| 2k |
| 1 |
| 2 |
| 1-2k |
| 2k |
则存在x∈(0,6]使g(x)<g(0)=75,所以k<
| 1 |
| 2 |
综上可知k≥
| 1 |
| 2 |
点评:本题考查了基本不等式,导数,在实际问题中的运用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设x、y满足
,则(x-1)2+(y-1)2的最小值是( )
|
A、
| ||||
B、
| ||||
| C、1 | ||||
| D、2 |
设
表示复数z的共轭复数,则与“复数z为实数”不等价的说法是( )
. |
| z |
A、z=
| ||
| B、z2≥0 | ||
C、z+
| ||
| D、lmz=0(lmz表示复数z的虚部) |
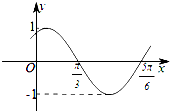 已知函数f(x)=sinωx+φ)(ω>0,0<φ≤
已知函数f(x)=sinωx+φ)(ω>0,0<φ≤