题目内容
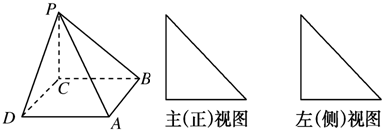
如图，在四棱锥P-ABCD中，底面为正方形，PC与底面ABCD垂直，图为该四棱锥的主视图和左视图，它们是腰长为6cm的全等的等腰直角三角形．
（Ⅰ）根据图所给的主视图、左视图，画出相应的俯视图，并求出该俯视图的面积；
（Ⅱ）求PA的长
（Ⅰ）根据图所给的主视图、左视图，画出相应的俯视图，并求出该俯视图的面积；
（Ⅱ）求PA的长
考点：由三视图求面积、体积,简单空间图形的三视图
专题：计算题,空间位置关系与距离
分析：（I）由直观图与四棱锥的主视图和左视图知，几何体的俯视图为（内含对角线）边长为6cm的正方形，由此可得其俯视图的面积；
（II）由（I）知侧棱PC垂直于底面，得△PAC为直角三角形，利用勾股定理计算PA长．
（II）由（I）知侧棱PC垂直于底面，得△PAC为直角三角形，利用勾股定理计算PA长．
解答：
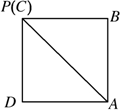
解：（Ⅰ）由直观图与四棱锥的主视图和左视图知，几何体的侧面PBC与侧面PCD都与底面ABCD垂直，侧棱PC垂直于底面，
∴侧面PBC与侧面PCD在底面ABCD的射影，分别是线段BC与CD，
∴几何体的俯视图为（内含对角线），边长为6cm的正方形，
如图，其面积为36（cm2）．
（Ⅱ）由（I）知侧棱PC垂直于底面，∴△PAC为直角三角形，
底面是正方形，AB=6，∴AC=6
．又PC=6
∴PA=
=
=6
（cm）
∴侧面PBC与侧面PCD在底面ABCD的射影，分别是线段BC与CD，
∴几何体的俯视图为（内含对角线），边长为6cm的正方形，
如图，其面积为36（cm2）．
（Ⅱ）由（I）知侧棱PC垂直于底面，∴△PAC为直角三角形，
底面是正方形，AB=6，∴AC=6
| 2 |
∴PA=
| AC2+PC2 |
| 72+36 |
| 3 |
点评：本题考查了几何体的三视图及由三视图求几何量，解题的关键是由三视图判断几何体的性质．
练习册系列答案
作业辅导系列答案
同步学典一课多练系列答案
相关题目
变速运动的物体的速度为v（t）=1-t2m/s（其中t为时间，单位：s），则它在前2s内所走过的路程为（ ）
A、-
| ||
B、
| ||
| C、-2 | ||
| D、2 |