题目内容
11.已知△ABC中,角A,B,C对应的分别是a,b,c,若a=4,b=6,C=60°.(1)求$\overrightarrow{BC}•\overrightarrow{CA}$;
(2)求$\overrightarrow{CA}$在$\overrightarrow{BC}$方向上的投影.
分析 (1)利用平面向量的数量积公式求得;
(2)利用平面向量的数量积公式的几何意义求得即可.
解答 解:(1)因为-a=4,b=6,C=60°.所以$\overrightarrow{BC}•\overrightarrow{CA}$=abcos(180°-60°)=4×6×($-\frac{1}{2}$)=-12;
(2)$\overrightarrow{CA}$在$\overrightarrow{BC}$方向上的投影为$|\overrightarrow{CA}|cos(180°-C)$=6×$(-\frac{1}{2})$=-3.
点评 本题考查了平面向量数量积的公式以及几何意义的运用;熟练掌握数量积公式的意义是关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
16.$cos\sqrt{2},sin\sqrt{2},tan\sqrt{2}$的大小关系是( )
| A. | $sin\sqrt{2}<cos\sqrt{2}<tan\sqrt{2}$ | B. | $cos\sqrt{2}<sin\sqrt{2}<tan\sqrt{2}$ | C. | $cos\sqrt{2}<tan\sqrt{2}<sin\sqrt{2}$ | D. | $sin\sqrt{2}<tan\sqrt{2}<cos\sqrt{2}$ |
3.函数f(x)=cos(3x+φ)的图象关于原点成中心对称,则φ等于( )
| A. | -$\frac{π}{2}$ | B. | 2kπ-$\frac{π}{2}$(k∈Z) | C. | kπ(k∈Z) | D. | kπ+$\frac{π}{2}$(k∈Z) |
1.如图所示,在△ABC中,BD=2CD,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$,则$\overrightarrow{AD}$=( )
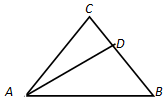

| A. | $\frac{2}{3}\overrightarrow a+\frac{1}{3}\overrightarrow b$ | B. | $\frac{2}{3}\overrightarrow a-\frac{1}{3}\overrightarrow b$ | C. | $\frac{1}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$ | D. | $\frac{2}{3}\overrightarrow a-\frac{2}{3}\overrightarrow b$ |

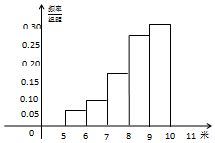 某市为了解今年高中毕业生的身体素质状况,从本市某校高中毕业班中抽取一个班进行实心球测试,成绩在8米及以上的为合格.把所得数据整理后,分成六组得到频率分布直方图的一部分(如图).已知前五个小组的频率分别为0.06.0.10,0.14,0.28,0.30.第六小组的频数是6.
某市为了解今年高中毕业生的身体素质状况,从本市某校高中毕业班中抽取一个班进行实心球测试,成绩在8米及以上的为合格.把所得数据整理后,分成六组得到频率分布直方图的一部分(如图).已知前五个小组的频率分别为0.06.0.10,0.14,0.28,0.30.第六小组的频数是6.