题目内容

在△ABC中，|AC|2=
BC
•
AC
，
BA
=（-2，-3），
BC
=（m，1），则m的值等于（　　）
A、8
B、-8
C、
2
3
D、-
2
3
考点：平面向量数量积的运算
专题：计算题,解三角形,平面向量及应用
分析：先求向量AC，再分别求出a，b，c的平方，运用向量的数量积的定义和余弦定理，化简|AC|2=
BC
•
AC
，得到b2=a2-c2，代入即可得到m的值．
解答： 解：由于
BA
=（-2，-3），
BC
=（m，1），
则
AC
=
BC
-
BA
=（m+2，4），
即有c2=13，a2=m2+1，b2=（m+2）2+16=m2+4m+20．
由|AC|2=
BC
•
AC
，得b2=abcosC=
1
2
（a2+b2-c2），
则b2=a2-c2，即有m2+4m+20=m2+1-13，
即4m=-32，即m=-8．
故选B．
点评：本题考查平面向量的数量积的定义和性质：向量的平方即模的平方，考查余弦定理的运用，以及运算能力，属于中档题．
练习册系列答案
相关题目
该茎叶图记录了甲、乙两组各五名学生在一次数学测试中的成绩（单位：分），已知甲组数据的平均数为87，乙组数据的中位数为87，则x，y的值分别为（　　）
A、2，6B、2，7
C、3，6D、3，7
函数f（x）=2lnx+2x-5的零点个数为（　　）
A、1B、2C、0D、3
如图，D为等腰三角形ABC底边AB的中点，则下列等式恒成立的是（　　）
A、
CA
•
CB
=0
B、
CD
•
AB
=0
C、
CA
•
CD
=0
D、
CD
•
CB
=0
在△ABC中，若（a2+c2-b2）sinB=
3
2
ac，则角B的值为（　　）
A、
π
6
或
π
3
B、
π
3
C、
π
6
D、
π
3
或
2π
3
已知函数f（x）=
1
3
x3-ax+1．
（1）若x=1时，f（x）取得极值，求实数a的值；
（2）求f（x）在[0，1]上的最小值．
已知定义在R上的函数f（x）=x2（ax-3）+2，其中a为常数．
（1）若x=1是函数y=f（x）的一个极值点，求a的值；
（2）当a＞0时，若g（x）=f（x）+f′（x），（其中x∈[0，2]），在x=2处取得最小值，求实数a的取值范围．
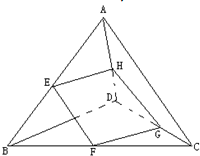已知E、F、G、H分别是空间四边形四条边AB、BC、CD、DA的中点，BD⊥AC．求证：四边形EFGH是矩形．
求函数y=2 
1-x
1+x
的值域．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网