题目内容
11.已知函数f(x)=$\frac{1}{3}$x3-alnx-$\frac{1}{3}$(a∈R,a≠0)(1)当a=3时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若对任意的x∈[1,+∞),都有f(x)≥0恒成立,求a的取值范围.
分析 (1)求出函数的导数,计算f(1),f′(1),求出切线方程即可;
(2)求出函数的导数,通过讨论a的范围,求出函数f(x)的最小值大于等于0,从而求出a的范围即可.
解答 解:(1)当a=3时,f(x)=$\frac{1}{3}$x3-3lnx-$\frac{1}{3}$,f(1)=0,
∴f′(x)=x2-$\frac{3}{x}$,∴f′(1)=-2,切点为(1,0),
∴曲线y=f(x)在点(1,f(1))处的切线方程为:
y-0=(-2)•(x-1),即2x+y-2=0.
(2)对任意的x∈[1,+∞),使f(x)≥0恒成立,
只需对任意的x∈[1,+∞),f(x)min≥0,
∴f′(x)=$\frac{{x}^{3}-a}{x}$,(x>0),
当a<0时,f′(x)>0恒成立,
∴函数f(x)的递增区间为(0,+∞);
当a>0时,令f′(x)=0,解得:x=$\root{3}{a}$或x=-$\root{3}{a}$(舍),
x,f′(x),f(x)的变化情况如下表:
| x | (0,$\root{3}{a}$) | $\root{3}{a}$ | ($\root{3}{a}$,+∞) |
| f′(x) | - | 0 | + |
| f(x) | 递减 | 极小值 | 递增 |
①当a<0时,函数f(x)在(1,+∞)上是增函数,
∴f(x)min=f(1)=$\frac{1}{3}$-aln1-$\frac{1}{3}$=0,∴a<0满足题意;
②当0<a≤1时,0<$\root{3}{a}$≤1,函数f(x)在(1,+∞)上是增函数,
∴f(x)min=f(1)=$\frac{1}{3}$-aln1-$\frac{1}{3}$=0,∴0<a≤1满足题意;
③当a>1时,$\root{3}{a}$>1,函数f(x)在(1,$\root{3}{a}$)上是减函数,在($\root{3}{a}$,+∞)上是增函数,
∴f(x)min=f($\root{3}{a}$)=$\frac{a-alna-1}{3}$<f(1)=0,
∴a>1不满足题意.
综上,a的取值范围为(-∞,0)∪(0,1].
点评 本题考查了切线方程问题,考查函数的单调性.最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.某几何体的三视图如图所示,则该几何体的体积是( )
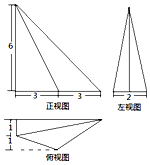

| A. | 10 | B. | 15 | C. | 18 | D. | 20 |
16.设z=1+i(i是虚数单位),O为坐标原点,若复数$\frac{2}{z}+{z^2}$在复平面内对应的向量为$\overrightarrow{OZ}$,则向量$\overrightarrow{OZ}$的模是( )
| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
3.在△ABC中,M是BC的中点,BM=2,AM=AB-AC,则△ABC的面积的最大值为( )
| A. | $2\sqrt{2}$ | B. | $2\sqrt{3}$ | C. | $3\sqrt{2}$ | D. | $3\sqrt{3}$ |
20. 执行如图所示的程序框图,则输出的结果是( )
执行如图所示的程序框图,则输出的结果是( )
 执行如图所示的程序框图,则输出的结果是( )
执行如图所示的程序框图,则输出的结果是( )| A. | 98 | B. | 99 | C. | 100 | D. | 101 |