题目内容
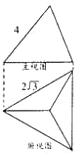已知正三棱锥P-ABC的主视图、俯视图如图所示，则该正三棱锥的左视图的面积为考点：简单空间图形的三视图
专题：空间位置关系与距离
分析：由题意可知，几何体的侧面是等腰三角形，要该三棱锥的左视图的面积，必须求出VA在左视图的射影的长度，即求V到底面的距离．
解答：
解：正三棱锥V-ABC的侧面是等腰三角形，底面是正三角形，底面上的高是3，
所以V到底面的距离：
=2
；
该三棱锥的左视图的面积：
×2
×2
=6
故答案为：6
所以V到底面的距离：
| 42-22 |
| 3 |
该三棱锥的左视图的面积：
| 1 |
| 2 |
| 3 |
| 3 |
故答案为：6
点评：本题考查三视图求面积，空间想象能力，是中档题．
练习册系列答案
全能测控期末小状元系列答案
智趣暑假温故知新系列答案
相关题目
已知点P（x，y）的坐标满足条件
，那么点P到直线3x-4y-13=0的最小值为（ ）
|
A、
| ||
| B、2 | ||
C、
| ||
| D、1 |
（x2+如图所示是一个算法的流程图，则输出p的值是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|