题目内容
已知(x2+
)6(k∈N*)的展开项的常数系数小于120,则k= .
| k |
| x |
考点:二项式定理的应用
专题:二项式定理
分析:利用二项展开式的通项公式求出第r+1项,令x的指数为0求出常数项,列出不等式解得.
解答:
解:(x2+
)6(k∈N*)的展开项的通项为
x2(6-r)(
)r=kr
x12-3r,当12-3r=0时,即r=4时,得常数项为k4
=15k4<120,k4<8,k∈N*,k=1;
故答案为:1.
| k |
| x |
| C | r 6 |
| k |
| x |
| C | r 6 |
| C | 4 6 |
故答案为:1.
点评:题考查二项展开式的通项公式是解决二项展开式的特定项问题的工具.

练习册系列答案
相关题目
已知向量
,
满足|
|=3,|
|=2
,且
⊥(
+
),则
在
方向上的投影为 ( )
| a |
| b |
| a |
| b |
| 3 |
| a |
| a |
| b |
| a |
| b |
A、-
| ||||
B、
| ||||
| C、-3 | ||||
| D、3 |
已知样本数据3,4,5,x,y的平均数是5,标准差是
,则xy=( )
| 2 |
| A、42 | B、40 | C、36 | D、30 |
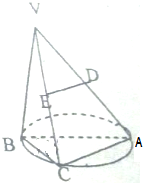 如图,AB是圆O的直径,AB=2,点C在圆O上,且∠ABC=60°,V到圆O所在的平面的距离为3,且VC垂直于圆O所在的平面,D,E分别是VA,VC的中点.
如图,AB是圆O的直径,AB=2,点C在圆O上,且∠ABC=60°,V到圆O所在的平面的距离为3,且VC垂直于圆O所在的平面,D,E分别是VA,VC的中点.
 如图,四棱锥P-ABCD的侧棱都相等,底面ABCD是正方形,O为对角线AC、BD的交点,PO=OA,求直线PA与面ABCD所成的角的大小.
如图,四棱锥P-ABCD的侧棱都相等,底面ABCD是正方形,O为对角线AC、BD的交点,PO=OA,求直线PA与面ABCD所成的角的大小.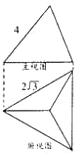 已知正三棱锥P-ABC的主视图、俯视图如图所示,则该正三棱锥的左视图的面积为
已知正三棱锥P-ABC的主视图、俯视图如图所示,则该正三棱锥的左视图的面积为