题目内容
设函数y=f(x)是定义在R上的偶函数,对任意x∈R,有f(x+6)=f(x)+f(3)成立,且f(-2)=-1,当x1,x2∈[0,3]且x1≠x2时,有
>0,给出下列命题:
①f(2012)=-1;
②x=-6是y=f(x)图象的一条对称轴;
③y=f(x)在[-9,-6]上是增函数;
④函数y=f(x)在[-9,9]上有4个零点.
正确命题的序号是( )
| f(x1)-f(x2) |
| x1-x2 |
①f(2012)=-1;
②x=-6是y=f(x)图象的一条对称轴;
③y=f(x)在[-9,-6]上是增函数;
④函数y=f(x)在[-9,9]上有4个零点.
正确命题的序号是( )
| A、①② | B、③④ |
| C、①②③④ | D、①②④ |
考点:命题的真假判断与应用
专题:函数的性质及应用
分析:由已知求出函数的周期为6,结合f(-2)=-1可求得f(2012)=-1;
由-12为周期及函数为偶函数求得直线x=-6是函数y=f(x)图象的一条对称轴;
由函数在[0,3]上为增函数及x=-6是函数y=f(x)图象的一条对称轴可得y=f(x)在[-9,-6]上为减函数;
由函数的增减性、对称性、奇偶性、周期及f(3)=0可得方程f(x)=0在[-9,9]上有4个根.
由-12为周期及函数为偶函数求得直线x=-6是函数y=f(x)图象的一条对称轴;
由函数在[0,3]上为增函数及x=-6是函数y=f(x)图象的一条对称轴可得y=f(x)在[-9,-6]上为减函数;
由函数的增减性、对称性、奇偶性、周期及f(3)=0可得方程f(x)=0在[-9,9]上有4个根.
解答:
解:由函数f(x)为偶函数可得,f(-3)=f(3),
∵f(x+6)=f(x)+f(3),
令x=-3可得,f(3)=f(-3)+f(3)=2f(3),
∴f(3)=0,
∴f(x+6)=f(x)+f(3)=f(x),即f(x+6)=f(x).
又f(-2)=-1.
①f(2012)=f(335×6+2)=f(2)=f(-2)=-1,
∴f(2012)=-1,①正确;
②由(x+6)=f(x),可知6为函数的周期,则-12为函数的周期,
∴f(-12+x)=f(x)=f(-x),则x=
=-6为函数的对称轴,②正确;
③由x1,x2∈[0,3]且x1≠x2时,都有
>0,0可知函数在[0,3]上为增函数,
则函数在[-6,-3]上为增函数,又x=-6为对称轴,则在[-9,-6]上为减函数,③正确;
④∵f(3)=0,
∴f(-3)=0,f(9)=f(6+3)=0,f(-9)=0,结合函数的周期为6及函数的增减性可得方程f(x)=0在[-9,9]上仅有4个根,④正确.
故正确命题为:①②④.
故选:D
∵f(x+6)=f(x)+f(3),
令x=-3可得,f(3)=f(-3)+f(3)=2f(3),
∴f(3)=0,
∴f(x+6)=f(x)+f(3)=f(x),即f(x+6)=f(x).
又f(-2)=-1.
①f(2012)=f(335×6+2)=f(2)=f(-2)=-1,
∴f(2012)=-1,①正确;
②由(x+6)=f(x),可知6为函数的周期,则-12为函数的周期,
∴f(-12+x)=f(x)=f(-x),则x=
| -12+x-x |
| 2 |
③由x1,x2∈[0,3]且x1≠x2时,都有
| f(x1)-f(x2) |
| x1-x2 |
则函数在[-6,-3]上为增函数,又x=-6为对称轴,则在[-9,-6]上为减函数,③正确;
④∵f(3)=0,
∴f(-3)=0,f(9)=f(6+3)=0,f(-9)=0,结合函数的周期为6及函数的增减性可得方程f(x)=0在[-9,9]上仅有4个根,④正确.
故正确命题为:①②④.
故选:D
点评:本题考查了命题的真假判断与应用,考查了函数的性质,训练了函数的单调性、奇偶性、周期性的用法,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

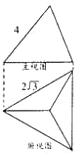 已知正三棱锥P-ABC的主视图、俯视图如图所示,则该正三棱锥的左视图的面积为
已知正三棱锥P-ABC的主视图、俯视图如图所示,则该正三棱锥的左视图的面积为