题目内容
已知函数f(x)=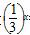 ,x∈[-1,1],函数g(x)=f 2(x)-2af(x)+3的最小值为h(a).
,x∈[-1,1],函数g(x)=f 2(x)-2af(x)+3的最小值为h(a).
(1)求h(a);
(2)是否存在实数m、n,同时满足以下条件:
①m>n>3;
②当h(a)的定义域为[n,m]时,值域为[n2,m2].
若存在,求出m、n的值;若不存在,说明理由.
(1)因为x∈[-1,1],所以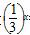 ∈
∈ .
.
设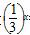 =t,t∈
=t,t∈ ,则g(x)=φ(t)=t2-2at+3=(t-a)2+3-a2.
,则g(x)=φ(t)=t2-2at+3=(t-a)2+3-a2.
当a<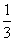 时,h(a)=φ
时,h(a)=φ =
= -
- ;
;
当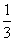 ≤a≤3时,h(a)=φ(a)=3-a2;
≤a≤3时,h(a)=φ(a)=3-a2;
当a>3时,h(a)=φ(3)=12-6a.
所以h(a)=
(2)因为m>n>3,a∈[n,m],所以h(a)=12-6a.
因为h(a)的定义域为[n,m],值域为[n2,m2],且h(a)为减函数,
所以 两式相减得6(m-n)=(m-n)(m+n),因为m>n,所以m-n≠0,得m+n=6,但这与“m>n>3”矛盾,故满足条件的实数m、n不存在.
两式相减得6(m-n)=(m-n)(m+n),因为m>n,所以m-n≠0,得m+n=6,但这与“m>n>3”矛盾,故满足条件的实数m、n不存在.

练习册系列答案
相关题目
 等于( )
等于( ) D.-
D.-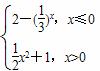 的图象恰好有3个不同的公共点,则实数m的取值范围是( )
的图象恰好有3个不同的公共点,则实数m的取值范围是( )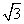 ,4) B.(
,4) B.(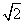 ,+∞)
,+∞) 则f(log43)=________.
则f(log43)=________. D.ln2
D.ln2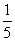 )x-log3x,若实数x0是方程f(x)=0的解,且0<x1<x0,则f(x1)的值( )
)x-log3x,若实数x0是方程f(x)=0的解,且0<x1<x0,则f(x1)的值( )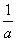 ,b) B.(10a,1-b)
,b) B.(10a,1-b)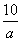 ,b+1) D.(a2,2b)
,b+1) D.(a2,2b)