题目内容
设函数f(x)=ax+bx-cx,其中c>a>0,c>b>0.
(1)记集合M={(a,b,c)|a,b,c不能构成一个三角形的三条边长,且a=b},则(a,b,c)∈M所对应的f(x)的零点的取值集合为________;
(2)若a,b,c是△ABC的三条边长,则下列结论正确的是________.(写出所有正确结论的序号)
①∀x∈(-∞,1),f(x)>0;
②∃x∈R,使ax,bx,cx不能构成一个三角形的三条边长;
③若△ABC为钝角三角形,则∃x∈(1,2),使f(x)=0.
(1){x|0<x≤1} (2)①②③
[解析] (1)∵c>a>0,c>b>0,a=b,且a、b、c不能构成三角形的三边,∴0<a+a≤c,∴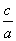 ≥2,
≥2,
令f(x)=0得,ax+bx=cx,∵a=b,∴2ax=cx,
∴(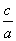 )x=2,∴x=log
)x=2,∴x=log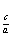 2,∴
2,∴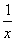 =log2
=log2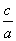 ≥1,∴0<x≤1.
≥1,∴0<x≤1.
(2)①∵a、b、c是三角形的三边长,∴a+b>c,∵c>a>0,c>b>0,∴0<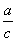 <1,0<
<1,0<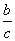 <1,∴当x∈(-∞,1)时,f(x)=ax+bx-cx=cx[(
<1,∴当x∈(-∞,1)时,f(x)=ax+bx-cx=cx[(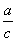 )x+(
)x+(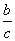 )x-1]>cx(
)x-1]>cx(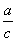 +
+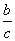 -1)=
-1)=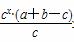 >0,∴①正确;
>0,∴①正确;
②令a=2,b=3,c=4,则a、b、c构成三角形的三边长,取x=2,则a2、b2、c2不能构成三角形的三边长,故②正确;
③∵c>a,c>b,△ABC为钝角三角形,∴a2+b2-c2<0,
又f(1)=a+b-c>0,f(2)=a2+b2-c2<0,
∴函数f(x)在(1,2)上存在零点,③正确.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 的图像( )
的图像( )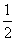 )x-2的图象交点为(x0,y0),则x0所在的区间为( )
)x-2的图象交点为(x0,y0),则x0所在的区间为( )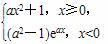 在(-∞,+∞)上单调,则a的取值范围是( )
在(-∞,+∞)上单调,则a的取值范围是( )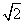 ]∪(1,
]∪(1,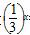 ,x∈[-1,1],函数g(x)=f 2(x)-2af(x)+3的最小值为h(a).
,x∈[-1,1],函数g(x)=f 2(x)-2af(x)+3的最小值为h(a).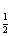 x|的图象是( )
x|的图象是( )
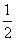 },则f(10x)>0的解集为( )
},则f(10x)>0的解集为( )