题目内容
下表是某种产品销售收入与销售量之间的一组数据:
(1)画出散点图;
(2)求出回归方程;
(3)根据回归方程估计销售量为9吨时的销售收入.
(参考公式:
=
=
,
=
-
)
| 销售量x(吨) | 2 | 3 | 5 | 6 |
| 销售收入y(千元) | 7 | 8 | 9 | 12 |
(2)求出回归方程;
(3)根据回归方程估计销售量为9吨时的销售收入.
(参考公式:
| ∧ |
| b |
| |||||||
|
| |||||
|
| ∧ |
| a |
. |
| y |
| ∧ |
| b |
. |
| x |
考点:线性回归方程
专题:概率与统计
分析:(1)直接画出散点图即可.
(2)根据参考数据,可求x,y之间的线性回归方程;
(3)x=9代入回归直线方程,即可求出销售量为9吨时的销售收入估计值.
(2)根据参考数据,可求x,y之间的线性回归方程;
(3)x=9代入回归直线方程,即可求出销售量为9吨时的销售收入估计值.
解答:
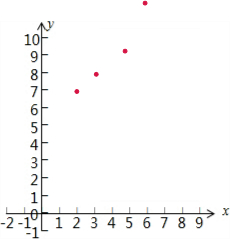 解:(1)由题意散点图如图:…4分
解:(1)由题意散点图如图:…4分
(2)根据参考数据
=
=4,
=
=9,
得b=
=
=1.1,…7分
a=
-b
=9-1.1×4=4.6,…9分
∴线性回归方程为y=1.1x+4.6.…10分.(3)当x=9时,y=9.9+4.6=14.5.
答:根据回归方程估计销售量为9吨时的销售收入约为14.5千元.
 解:(1)由题意散点图如图:…4分
解:(1)由题意散点图如图:…4分(2)根据参考数据
. |
| x |
| 2+3+5+6 |
| 4 |
. |
| y |
| 7+8+9+12 |
| 4 |
得b=
| |||||||
|
| 155-144 |
| 74-64 |
a=
. |
| y |
. |
| x |
∴线性回归方程为y=1.1x+4.6.…10分.(3)当x=9时,y=9.9+4.6=14.5.
答:根据回归方程估计销售量为9吨时的销售收入约为14.5千元.
点评:本题主要考查回归分析,散点图的作法,考查运算能力、应用意识,属于基础题.

练习册系列答案
相关题目
若两条直线y=a2x-1与y=(a+2)x-a+1互相平行,则a等于( )
| A、2 | B、1 | C、-2 | D、-1 |
已知△ABC中,A、B、C的对边分别为a、b、c,若A=30°,C=105°,b=8,则a等于( )
| A、4 | ||
B、4
| ||
C、4
| ||
D、4
|

 如图,椭圆C:
如图,椭圆C: