题目内容
直角△A1B1C1的斜边为A1B1，面积为S1，直角△A2B2C2的斜边为A2B2，面积为S2，若△A1B1C1∽△A2B2C2，A1B1：A2B2=1：2，则S1：S2等于（ ）
| A、2：1 | ||
| B、1：2 | ||
C、1：
| ||
| D、1：4 |
考点：相似三角形的性质
专题：选作题,立体几何
分析：利用三角形相似，面积比等于相似比的平方，即可得出结论．
解答：
解：∵△A1B1C1∽△A2B2C2，A1B1：A2B2=1：2，
∴S1：S2=1：4．
故选：D．
∴S1：S2=1：4．
故选：D．
点评：本题考查相似三角形的性质，利用三角形相似，面积比等于相似比的平方是关键．
练习册系列答案
相关题目
设有一个回归方程为y=2-3x，变量x增加1个单位时，则y平均（ ）
| A、增加2个单位 |
| B、减少2个单位 |
| C、增加3个单位 |
| D、减少3个单位 |
已知点A（-3，1，4），则点A关于x轴的对称点的坐标为（ ）
| A、（-3，1，-4） |
| B、（3，-1，-4） |
| C、（-3，-1，-4） |
| D、（-3，1，-4） |
已知z=-
，则1+z50+z100的值为（ ）
| 1+i | ||
|
| A、i | B、1 | C、2+i | D、3 |
| ∫ | 2 1 |
| 2 |
| x |
| A、e2-2ln2 |
| B、e2-e-2ln2 |
| C、e2+e+2ln2 |
| D、e2-e+2ln2 |
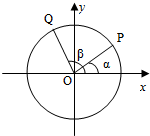如图，以Ox为始边分别作角α与β（0＜α＜β＜π），它们的终边分别与单位圆相交于点P、Q，已知点P的坐标为（