题目内容
如图，在山底测得山顶仰角∠CAB=45°，沿倾斜角为30°的斜坡走1000米至S点，又测得山顶仰角为75°，求山高BC．考点：解三角形的实际应用
专题：应用题,解三角形
分析：作出图形，过点S作SE⊥AC于E，SH⊥AB于H，依题意可求得SE在△BDS中利用正弦定理可求BD的长，从而可得山顶高BC．
解答：
解：依题意，过S点作SE⊥AC于E，SH⊥AB于H，
∵∠SAE=30°，AS=1000米，
∴CD=SE=AS•sin30°=500米，
依题意，在Rt△HAS中，∠HAS=45°-30°=15°，
∴HS=AS•sin15°，
在Rt△BHS中，∠HBS=30°，
∴BS=2HS=2000sin15°，
在Rt△BSD中，BD=BS•sin75°=2000sin15°•sin75°
=2000sin15°•cos15°=1000×sin30°=500米．
∴BC=BD+CD=1000米．
解：依题意，过S点作SE⊥AC于E，SH⊥AB于H，∵∠SAE=30°，AS=1000米，
∴CD=SE=AS•sin30°=500米，
依题意，在Rt△HAS中，∠HAS=45°-30°=15°，
∴HS=AS•sin15°，
在Rt△BHS中，∠HBS=30°，
∴BS=2HS=2000sin15°，
在Rt△BSD中，BD=BS•sin75°=2000sin15°•sin75°
=2000sin15°•cos15°=1000×sin30°=500米．
∴BC=BD+CD=1000米．
点评：本题考查正弦定理的应用，考查作图与计算的能力，属于中档题．
练习册系列答案
相关题目
已知点A（-3，1，4），则点A关于x轴的对称点的坐标为（ ）
| A、（-3，1，-4） |
| B、（3，-1，-4） |
| C、（-3，-1，-4） |
| D、（-3，1，-4） |
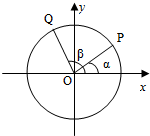如图，以Ox为始边分别作角α与β（0＜α＜β＜π），它们的终边分别与单位圆相交于点P、Q，已知点P的坐标为（
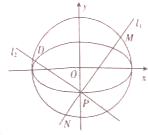已知椭圆E：