题目内容
已知M(2,2
)为抛物线C:y2=2px(p>0)上一点
(1)求抛物线C的标准方程;
(2)设A、B抛物线C上异于原点O的两点且∠AOB=90°,求证:直线AB恒过定点,并求出该定点坐标;
(3)在(2)的条件下,若过原点O向直线AB作垂线,求垂足P(x,y)的轨迹方程.
| 2 |
(1)求抛物线C的标准方程;
(2)设A、B抛物线C上异于原点O的两点且∠AOB=90°,求证:直线AB恒过定点,并求出该定点坐标;
(3)在(2)的条件下,若过原点O向直线AB作垂线,求垂足P(x,y)的轨迹方程.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由M(2,2
)为抛物线C:y2=2px(p>0)上一点,能求出p=2,由此能求出抛物线C的标准方程.
(2)设直线l:y=kx+m,A(x1,y1),B(x2,y2),联立y2=4x,得k2x2+(2km-4)x+m2=0,由此利用韦达定理、向量知识结合已知条件能证明直线恒过定点N(4,0).
(3)由已知条件推导出P点在以ON为直径的圆周上(除去原点),由此能求出点P的轨迹方程.
| 2 |
(2)设直线l:y=kx+m,A(x1,y1),B(x2,y2),联立y2=4x,得k2x2+(2km-4)x+m2=0,由此利用韦达定理、向量知识结合已知条件能证明直线恒过定点N(4,0).
(3)由已知条件推导出P点在以ON为直径的圆周上(除去原点),由此能求出点P的轨迹方程.
解答:
(1)解:∵M(2,2
)为抛物线C:y2=2px(p>0)上一点,
∴(2
)2=2p•2,解得p=2,
∴抛物线C的标准方程为y2=4x.(3分)
(2)证明:当直线的斜率存在时,
设直线l:y=kx+m,A(x1,y1),B(x2,y2),
联立y2=4x,得k2x2+(2km-4)x+m2=0,
依题意有k≠0,x1+x2=-
,且x1x2=
,
则∠AOB=90°,
∴
•
=x1x2+y1y2
=x1x2+(kx1+m)(kx2+m)
=(1+k2)x1x2+km(x1+x2)+m2=0,
(1+k2)
+km(-
)+m2=0,
化简得m2+4km=0,
∴m=-4k,此时直线l:y=kx-4k=(x-4)k,恒过点N(4,0)
当直线l的斜率不存在时,
设l:x=t,解得t=4,∴直线恒过定点N(4,0).(8分)
(3)解:过原点O向直线AB:y=k(x-4)垂线,垂中为P,
则P点在以ON为直径的圆周上(除去原点),
∵O(0,0),N(4,0),
∴点P的轨迹方程为:(x-2)2+y2=4(x≠0).(12分)
| 2 |
∴(2
| 2 |
∴抛物线C的标准方程为y2=4x.(3分)
(2)证明:当直线的斜率存在时,
设直线l:y=kx+m,A(x1,y1),B(x2,y2),
联立y2=4x,得k2x2+(2km-4)x+m2=0,
依题意有k≠0,x1+x2=-
| 2km-4 |
| k2 |
| m2 |
| k2 |
则∠AOB=90°,
∴
| OA |
| OB |
=x1x2+(kx1+m)(kx2+m)
=(1+k2)x1x2+km(x1+x2)+m2=0,
(1+k2)
| m2 |
| k2 |
| 2km-4 |
| k2 |
化简得m2+4km=0,
∴m=-4k,此时直线l:y=kx-4k=(x-4)k,恒过点N(4,0)
当直线l的斜率不存在时,
设l:x=t,解得t=4,∴直线恒过定点N(4,0).(8分)
(3)解:过原点O向直线AB:y=k(x-4)垂线,垂中为P,
则P点在以ON为直径的圆周上(除去原点),
∵O(0,0),N(4,0),
∴点P的轨迹方程为:(x-2)2+y2=4(x≠0).(12分)
点评:本题考查抛物线的标准方程的求法,考查直线过定点的证明,考查垂足的轨迹方程的求法,解题时要认真审题,注意向量知识的合理运用.

练习册系列答案
相关题目
 在平面直角坐标系xOy中,过点P(-4,0)作直线交椭圆C:
在平面直角坐标系xOy中,过点P(-4,0)作直线交椭圆C: 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,且PA⊥底面ABCD,BD⊥PC,E是PA的中点.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,且PA⊥底面ABCD,BD⊥PC,E是PA的中点.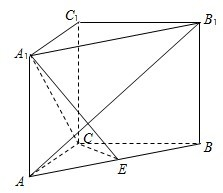 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=CB=CC1=2,E是AB中点.
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=CB=CC1=2,E是AB中点.