题目内容
 在平面直角坐标系xOy中,过点P(-4,0)作直线交椭圆C:
在平面直角坐标系xOy中,过点P(-4,0)作直线交椭圆C:| x2 |
| a2 |
| y2 |
| 3 |
| PB |
| PA |
(1)求实数a的值;
(2)若λ=2,求线段BB′的长;
(3)证明:
| B′F |
| FA |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)由焦点坐标可知c=1,又c2=a2-b2,b2=3,可求a;
(2)当λ=2时,由
=2
,知A为PB的中点,设A(x0,y0),则B(2x0+4,2y0),分别爱人椭圆方程可得方程组,解出y0即得;
(3)设A(x1,y1),B(x2,y2),则B′(x2,-y2),由
=λ
可得x2+4=λ(x1+4),y2=λy1①,而
,③-②×λ2得
+
=1-λ2④,①代入④得-1-x2-λ(x1+1)=0,可证明
-λ
=(0,0).
(2)当λ=2时,由
| PB |
| PA |
(3)设A(x1,y1),B(x2,y2),则B′(x2,-y2),由
| PB |
| PA |
|
| (x2-λx1)(x2+λx1) |
| 4 |
| y22-λ2y12 |
| 3 |
| B′F |
| FA |
解答:
解:(1)依题意,c=1,
又c2=a2-b2,其中b2=3,
∴a=2.
(2)当λ=2时,
=2
,即A为PB的中点,
设A(x0,y0),则B(2x0+4,2y0),
此时
+
=1,且
+
=1,
解得x0=-
,y0=±
,
∴线段BB′的长为
;
(3)设A(x1,y1),B(x2,y2),则B′(x2,-y2),
由
=λ
得(x2+4,y2)=λ(x1+4,y1),则x2+4=λ(x1+4),y2=λy1,①
又
,
③-②×λ2得
+
=1-λ2,④
将①代入④得-1-x2-λ(x1+1)=0,
则
-λ
=(-1-x2-λ(x1+1),y2-λy1)=(0,0),即证明
=λ
.
又c2=a2-b2,其中b2=3,
∴a=2.
(2)当λ=2时,
| PB |
| PA |
设A(x0,y0),则B(2x0+4,2y0),
此时
| x02 |
| 4 |
| y02 |
| 3 |
| (2x0+4)2 |
| 4 |
| (2y0)2 |
| 3 |
解得x0=-
| 7 |
| 4 |
3
| ||
| 8 |
∴线段BB′的长为
3
| ||
| 4 |
(3)设A(x1,y1),B(x2,y2),则B′(x2,-y2),
由
| PB |
| PA |
又
|
③-②×λ2得
| (x2-λx1)(x2+λx1) |
| 4 |
| y22-λ2y12 |
| 3 |
将①代入④得-1-x2-λ(x1+1)=0,
则
| B′F |
| FA |
| B′F |
| FA |
点评:本题考查椭圆方程的求解、直线与椭圆的位置关系、平面向量的运算等知识,考查方程思想,考查学生的推理论证与运算能力.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
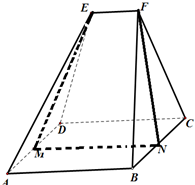 木工技艺是我国传统文化瑰宝之一,体现了劳动人民的无穷智慧.很多古代建筑和家具不用铁钉,保存到现代却依然牢固,这其中,有连接加固功能的“楔子”发挥了重要作用;如图,是一个楔子形状的直观图.其底面ABCD为一个矩形,其中AB=6,AD=4.顶部线段EF∥平面ABCD,棱EA=ED=FB=FC=6
木工技艺是我国传统文化瑰宝之一,体现了劳动人民的无穷智慧.很多古代建筑和家具不用铁钉,保存到现代却依然牢固,这其中,有连接加固功能的“楔子”发挥了重要作用;如图,是一个楔子形状的直观图.其底面ABCD为一个矩形,其中AB=6,AD=4.顶部线段EF∥平面ABCD,棱EA=ED=FB=FC=6