题目内容
2.斜率是1的直线与椭圆${x^2}+\frac{y^2}{4}=1$交于A、B两点,P为线段AB上的点,且AP=2PB,则点P的轨迹方程是148x2+13y2+64xy-20=0(在椭圆内).分析 设直线l的方程,代入椭圆方程,由x1,x2是方的两个根,分别求得x1,x2,由AP=2PB,求得x′=$\frac{{x}_{1}+2{x}_{2}}{3}$,代入即可即可求得P的轨迹方程.
解答 解:设动点为P(x′,y′),则过y=x+(y′-x′)$\left\{\begin{array}{l}{y=x+(y′-x′)}\\{{x}^{2}+\frac{{y}^{2}}{4}=1}\end{array}\right.$,整理得:5x2+2(y′-x′)x+(y′-x′)2-4=0,(※)
若直线l椭圆交于A(x1,y1),B(x2,y2),x1<x2,则x1,x2是方程(※)的两个根,且
x1=$\frac{-(y′-x′)-2\sqrt{5-(y′-x′)^{2}}}{5}$,①
x2=$\frac{-(y′-x′)+2\sqrt{5-(y′-x′)^{2}}}{5}$,②
由AP=2PB,x1<x2,则x′=$\frac{{x}_{1}+2{x}_{2}}{3}$,
代入整理得:4x′+y′=$\frac{2}{3}$$\sqrt{5-(y′-x′)^{2}}$,丨y′-x′丨<$\sqrt{5}$,
两边同时平方:148x′2+13y′2+64x′y′-20=0,
∴点P的轨迹方程148x2+13y2+64xy-20=0(在椭圆内).
故答案为:148x2+13y2+64xy-20=0(在椭圆内).
点评 本题考查直线与椭圆的位置关系,轨迹方程求法,考查计算能力,属于中档题.

练习册系列答案
相关题目
4.已知$\vec a=(x,4),\vec b=(3,2)$,$\vec a∥\vec b,则x$=( )
| A. | -6 | B. | $-\frac{3}{8}$ | C. | 6 | D. | $\frac{3}{8}$ |
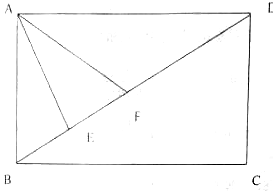 小王大学毕业后决定利用所学知识自主创业,在一块矩形的空地上办起了养殖场,如图所示,四边形ABCD为矩形,AB=200米,AD=200$\sqrt{3}$米,现为了养殖需要,在养殖场内要建造蓄水池,小王因地制宜,建造了一个三角形形状的蓄水池,其中顶点分别为A,E,F(E,F两点在线段BD上),且∠EAF=$\frac{π}{6}$,设∠BAE=α.
小王大学毕业后决定利用所学知识自主创业,在一块矩形的空地上办起了养殖场,如图所示,四边形ABCD为矩形,AB=200米,AD=200$\sqrt{3}$米,现为了养殖需要,在养殖场内要建造蓄水池,小王因地制宜,建造了一个三角形形状的蓄水池,其中顶点分别为A,E,F(E,F两点在线段BD上),且∠EAF=$\frac{π}{6}$,设∠BAE=α.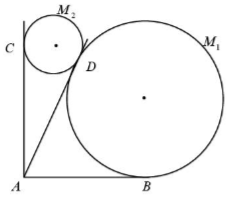 某景区欲建两条圆形观景步道M1,M2(宽度忽略不计),如图所示,已知AB⊥AC,AB=AC=AD=60(单位:米),要求圆M与AB,AD分别相切于点B,D,圆M2与AC,AD分别相切于点C,D.
某景区欲建两条圆形观景步道M1,M2(宽度忽略不计),如图所示,已知AB⊥AC,AB=AC=AD=60(单位:米),要求圆M与AB,AD分别相切于点B,D,圆M2与AC,AD分别相切于点C,D.