题目内容
5.设函数f(x)在R上存在导函数f′(x),对于任意的实数x,都有f(x)=4x2-f(-x),当x∈(-∞,0)时,f′(x)<4x,若f(m+1)≤f(-m)+4m+2,则实数m的取值范围是( )| A. | [-$\frac{1}{2}$,+∞) | B. | [-$\frac{3}{2}$,+∞) | C. | [-1,+∞) | D. | [-2,+∞) |
分析 利用构造法设g(x)=f(x)-2x2,推出g(x)为奇函数,判断g(x)的单调性,然后推出不等式得到结果.
解答 解:∵f(x)=4x2-f(-x),
∴f(x)-2x2+f(-x)-2x2=0,
设g(x)=f(x)-2x2,则g(x)+g(-x)=0,
∴函数g(x)为奇函数.
∵x∈(-∞,0)时,f′(x)<4x,
g′(x)=f′(x)-4x<0,
故函数g(x)在(-∞,0)上是减函数,
故函数g(x)在(0,+∞)上也是减函数,
若f(m+1)≤f(-m)+4m+2,
则f(m+1)-2(m+1)2≤f(-m)-2m2,
即g(m+1)≤g(-m),
∴m+1≥-m,解得:m≥-$\frac{1}{2}$,
故选:A.
点评 本题考查函数奇偶性、单调性、导数的综合应用,考查分析问题解决问题的能力,难度比较大.

练习册系列答案
相关题目
15.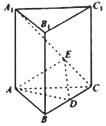 在底面为正三角形的直棱柱(侧棱垂直于底面的棱柱)ABC-A1B1C1中,AB=2,AA1=3,点D为棱BD的中点,点E为A,C上的点,且满足A1E=mEC(m∈R),当二面角E-AD-C的余弦值为$\frac{\sqrt{10}}{10}$时,实数m的值为( )
在底面为正三角形的直棱柱(侧棱垂直于底面的棱柱)ABC-A1B1C1中,AB=2,AA1=3,点D为棱BD的中点,点E为A,C上的点,且满足A1E=mEC(m∈R),当二面角E-AD-C的余弦值为$\frac{\sqrt{10}}{10}$时,实数m的值为( )
 在底面为正三角形的直棱柱(侧棱垂直于底面的棱柱)ABC-A1B1C1中,AB=2,AA1=3,点D为棱BD的中点,点E为A,C上的点,且满足A1E=mEC(m∈R),当二面角E-AD-C的余弦值为$\frac{\sqrt{10}}{10}$时,实数m的值为( )
在底面为正三角形的直棱柱(侧棱垂直于底面的棱柱)ABC-A1B1C1中,AB=2,AA1=3,点D为棱BD的中点,点E为A,C上的点,且满足A1E=mEC(m∈R),当二面角E-AD-C的余弦值为$\frac{\sqrt{10}}{10}$时,实数m的值为( )| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | 3 |
16.若点P对应的复数z满足|z|≤1,则P的轨迹是( )
| A. | 直线 | B. | 线段 | C. | 圆 | D. | 单位圆以及圆内 |
20.下表是降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据,根据表中提供的数据,求出y关于x的线性回归方程为y=0.7x+0.35,则表中m的值为( )
| x | 3.5 | 4.5 | 5.5 | 6.5 |
| y | 3 | 4m | 4 | 5 |
| A. | 1 | B. | 0.85 | C. | 0.95 | D. | 0.9 |
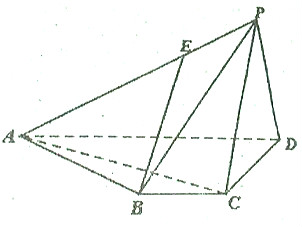 如图,四棱锥P-ABCD中,BC∥AD,BC=1,AD=3,AC⊥CD,且平面PCD⊥平面ABCD.
如图,四棱锥P-ABCD中,BC∥AD,BC=1,AD=3,AC⊥CD,且平面PCD⊥平面ABCD.