题目内容
10．若关于x的不等式|ax-2|＜3的解集为{x|-$\frac{5}{3}$＜x＜$\frac{1}{3}$}，则a=（ ）| A． | -2 | B． | 2 | C． | 3 | D． | -3 |
分析 解绝对值不等式，根据不等式的解集求出a的值即可．
解答 解：由|ax-2|＜3，得：-3＜ax-2＜3，
故-1＜ax＜5，
由不等式的解集是{x|-$\frac{5}{3}$＜x＜$\frac{1}{3}$}，
故a=-3，
故选：D．
点评 本题考查了解绝对值不等式问题，考查对应思想，是一道基础题．
练习册系列答案
名校通行证有效作业系列答案
相关题目
20．
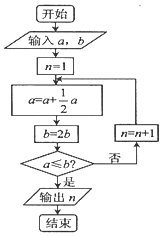宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题：松长五尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等．如图是源于其思想的一个程序框图，若输入的a，b分别为3，2，则输出的n=（ ）
宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题：松长五尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等．如图是源于其思想的一个程序框图，若输入的a，b分别为3，2，则输出的n=（ ）| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
5．设函数f（x）在R上存在导函数f′（x），对于任意的实数x，都有f（x）=4x2-f（-x），当x∈（-∞，0）时，f′（x）＜4x，若f（m+1）≤f（-m）+4m+2，则实数m的取值范围是（ ）
| A． | [-$\frac{1}{2}$，+∞） | B． | [-$\frac{3}{2}$，+∞） | C． | [-1，+∞） | D． | [-2，+∞） |
15．已知集合A={x|x＞-1}，B={x|x2+2x-3＜0}则A∩B=（ ）
| A． | （-1，3） | B． | （-1，1） | C． | （-1，+∞） | D． | （-3，1） |
2．某化肥厂生产甲、乙两种混合肥料，需要A，B，C三种主要原料，生产1车皮甲种肥料和生产1车皮乙种肥料所需三种原料的吨数如下表所示：
现有A种原料200吨，B种原料360吨，C种原料300吨，在此基础上生产甲、乙两种肥料．已知生产1车皮甲种肥料，产生的利润为2万元；生产1车皮乙种肥料，产生的利润为3万元、分别用x，y表示计划生产甲、乙两种肥料的车皮数．
（Ⅰ）用x，y列出满足生产条件的数学关系式，并画出相应的平面区域；
（Ⅱ）问分别生产甲、乙两种肥料各多少车皮，能够产生最大的利润？并求出此最大利润．
| 肥料 原料 | A | B | C |
| 甲 | 4 | 8 | 3 |
| 乙 | 5 | 5 | 10 |
（Ⅰ）用x，y列出满足生产条件的数学关系式，并画出相应的平面区域；
（Ⅱ）问分别生产甲、乙两种肥料各多少车皮，能够产生最大的利润？并求出此最大利润．
15．已知直线ax-by-2=0与曲线y=x2在点P（1，1）处的切线互相垂直，则$\frac{a}{b}$为（ ）
| A． | $\frac{2}{3}$ | B． | -$\frac{2}{3}$ | C． | $\frac{1}{2}$ | D． | -$\frac{1}{2}$ |