题目内容
平面上三点A、B、C满足|
|=1，|
|=1，|
|=
，则
•
+
•
+
•
= ．
| AB |
| BC |
| CA |
| 2 |
| AB |
| BC |
| BC |
| CA |
| CA |
| AB |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由平面上三点A、B、C满足|
|=1，|
|=1，|
|=
，可得|
|2+|
|2=2=|
|2，利用勾股定理的逆定理可得∠B=90°，∠A=∠C=45°．再利用数量积运算即可得出．
| AB |
| BC |
| CA |
| 2 |
| AB |
| BC |
| CA |
解答：
解：∵平面上三点A、B、C满足|
|=1，|
|=1，|
|=
，
∴|
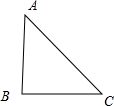
|2+|
|2=2=|
|2，
∴∠B=90°，∠A=∠C=45°．
如图所示，
∴
•
+
•
+
•
=0-
•
-
•
=-|
|2-|
|2=-1-1=-2．
故答案为：-2．
| AB |
| BC |
| CA |
| 2 |
∴|
| AB |
| BC |
| CA |
∴∠B=90°，∠A=∠C=45°．
如图所示，
∴
| AB |
| BC |
| BC |
| CA |
| CA |
| AB |
| CB |
| CA |
| AC |
| AB |
| CB |
| AB |
故答案为：-2．
点评：本题考查了勾股定理的逆定理、数量积运算，属于基础题．
练习册系列答案
相关题目
如图，四边形ABCD是边长为2的正方形，△ABE为等腰三角形，AE=BE，平面ABCD⊥平面ABE，动点F在CE上，无论点F运动到何处时，总有BF⊥AE．
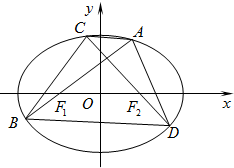已知椭圆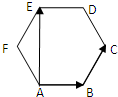
如图，在边长为1的正六边形ABCDEF中，