题目内容
已知正实数x，y满足x2+y2+xy=1，则x+y的最大值是 ．
考点：直线与圆的位置关系
专题：计算题,直线与圆
分析：利用基本不等式，根据xy≤
，把题设等式整理成关于x+y的不等式，求得其范围，则x+y的最大值可得．
| (x+y)2 |
| 4 |
解答：
解：∵x2+y2+xy=1
∴（x+y）2=1+xy
∵xy≤
∴（x+y）2-1≤
，
整理求得-
≤x+y≤
，
∴x+y的最大值是
．
故答案为：
．
∴（x+y）2=1+xy
∵xy≤
| (x+y)2 |
| 4 |
∴（x+y）2-1≤
| (x+y)2 |
| 4 |
整理求得-
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
∴x+y的最大值是
| 2 |
| 3 |
| 3 |
故答案为：
| 2 |
| 3 |
| 3 |
点评：本题主要考查了基本不等式．应熟练掌握如均值不等式，柯西不等式等性质．
练习册系列答案
相关题目
黑白两种颜色的六方边形地砖按图示的规律拼成若干个图案，则第n个图案中白色地砖的块数是（ ）
| A、3n+4 | B、4n+2 |
| C、5n-1 | D、6n |
设以a=(
)x，b=(
)x-1，c=log
x，若x＞l，则a，b，c的大小关系是（ ）
| 3 |
| 4 |
| 4 |
| 3 |
| 3 |
| 4 |
| A、a＜b＜c |
| B、c＜a＜b |
| C、b＜a＜c |
| D、b＜c＜a |
若△ABC的内角A、B、C的对边分别为a、b、c，且（a-b）2=c2-4，C=120°，则ab的值为（ ）
| A、4 | ||
B、
| ||
C、
| ||
D、8-4
|
如图所示，为了测量某湖泊两侧A，B间的距离，李宁同学首先选定了与A，B不共线的一点C，然后给出了三种测量方案：（△ABC的角A，B，C所对的边分别记为a，b，c）：①测量A，C，b；②测量a，b，C；③测量A，a，b则一定能确定A，B间距离的所有方案的序号为（ ）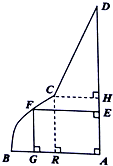
如图是一块镀锌铁皮的边角料ABCD，其中AB、CD、DA都是线段，曲线段BC是抛物线的一部分，且点B是该抛物线的顶点，BA所在直线是该抛物线的对称轴，经测量，AB=2米，AD=3米，AB⊥AD，点C到AD、AB的距离CH、CR的长均为1米，现要用这块边角料截一个矩形AEFG（其中点F在曲线段BC或线段CD上，点E在线段AD上，点G在线段AB上）．设BG的长为x米，矩形AEFG的面积为S平方米．