题目内容
下列结论正确的是（ ）
A、若向量
| ||||||||||||
B、已知向量
| ||||||||||||
C、“若θ=
| ||||||||||||
| D、若命题p：?x∈R，x2-x+1＜0，则￢p：?x∈R，x2-x+1＞0 |
考点：命题的真假判断与应用
专题：综合题,简易逻辑
分析：根据向量共线定理判断A，向量
，
为非零向量，则“
，
的夹角为钝角”的充要条件是“
•
＜0，且向量
，
不共线”，可判断B，条件否定，结论否定，可判断C；命题p：?x∈R，x2-x+1＜0，则￢p：?x∈R，x2-x+1≤0，可判断D．
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
解答：
解：若向量
∥
，
≠
，则存在唯一的实数λ使
=λ
，故A不正确；
已知向量
，
为非零向量，则“
，
的夹角为钝角”的充要条件是“
•
＜0，且向量
，
不共线”，故不正确；
条件否定，结论否定，可知C正确；
若命题p：?x∈R，x2-x+1＜0，则￢p：?x∈R，x2-x+1≤0，故D不正确．
故选：C．
| a |
| b |
| b |
| 0 |
| a |
| b |
已知向量
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
条件否定，结论否定，可知C正确；
若命题p：?x∈R，x2-x+1＜0，则￢p：?x∈R，x2-x+1≤0，故D不正确．
故选：C．
点评：本题考查命题的真假判断与应用，考查学生分析解决问题的能力，知识综合性强．
练习册系列答案
相关题目
要得到函数g（x）=cos2x的图象，只需将f（x）=sin（2x+
）的图象（ ）
| 5π |
| 6 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
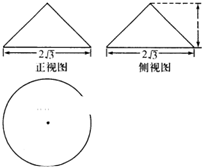
某几何体的三视图如图所示，则该几何体外接球的表面积为（ ）
A、
| ||
B、
| ||
| C、4π | ||
| D、16π |
某程序框图如图所示，现输入下列四个函数：f（x）=| 1 |
| x |
A、f（x）=
| ||
| B、f（x）=log3（x2+1） | ||
| C、f（x）=2x+2-x | ||
| D、f（x）=2x-2-x |
已知角α的终边经过点P（m，4），且cosα=-
，则m等于（ ）
| 3 |
| 5 |
A、-
| ||
| B、-3 | ||
C、
| ||
| D、3 |
如果直线ax+by=4与圆C：x2+y2=4相离，那么点P（a，b）与圆C的位置关系是（ ）
| A、在圆内 | B、在圆上 |
| C、在圆外 | D、不确定 |
已知等差数列{an}，a2+a18=36，则a5+a6+…+a15=（ ）
| A、130 | B、198 |
| C、180 | D、156 |