题目内容
17.若椭圆ax2+by2=1与直线x+y=1交于A,B两点,M为AB的中点,直线OM(O为原点)的斜率为2,又OA⊥OB,求a,b的值.分析 设A(x1,y1),B(x2,y2),M($\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{{y}_{1}+{y}_{2}}{2}$).联立$\left\{\begin{array}{l}{a{x}^{2}+b{y}^{2}=1}\\{x+y=1}\end{array}\right.$,得(a+b)x2-2bx+b-1=0.由韦达定理得M($\frac{b}{a+b}$,$\frac{a}{a+b}$).由kOM=2,得a=2b,由OA⊥OB,得a+b=2.由此能求出a,b.
解答 解:设A(x1,y1),B(x2,y2),M($\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{{y}_{1}+{y}_{2}}{2}$).
联立$\left\{\begin{array}{l}{a{x}^{2}+b{y}^{2}=1}\\{x+y=1}\end{array}\right.$,得(a+b)x2-2bx+b-1=0.
∴$\frac{{x}_{1}+{x}_{2}}{2}$=$\frac{b}{a+b}$,$\frac{{y}_{1}+{y}_{2}}{2}$=1-$\frac{{x}_{1}+{x}_{2}}{2}$=$\frac{a}{a+b}$.
∴M($\frac{b}{a+b}$,$\frac{a}{a+b}$).
∵kOM=2,∴a=2b.①
∵OA⊥OB,∴$\frac{{y}_{1}}{{x}_{1}}•\frac{{y}_{2}}{{x}_{2}}$=-1.
∴x1x2+y1y2=0.
∵x1x2=$\frac{b-1}{a+b}$,y1y2=(1-x1)(1-x2),
∴y1y2=1-(x1+x2)+x1x2
=1-$\frac{2b}{a+b}$+$\frac{b-1}{a+b}$=$\frac{a-1}{a+b}$.
∴$\frac{b-1}{a+b}+\frac{a-1}{a+b}$=0.
∴a+b=2.②
由①②得a=$\frac{4}{3}$,b=$\frac{2}{3}$.
点评 本题考查实数值的求法,是中档题,解题时要认真审题,注意椭圆、直线方程、直线垂直、韦达定理、中点坐标公式等知识点的灵活运用运用.

| A. | (2,+∞) | B. | (4,+∞) | C. | [2,4] | D. | (2,4] |
| A. | $\frac{43}{48}$ | B. | $-\frac{11}{24}$ | C. | $\frac{29}{36}$ | D. | $\frac{11}{48}$ |
| A. | (-∞,1]∪[3,+∞) | B. | (-∞,1)∪(3,+∞) | C. | [1,3] | D. | (1,3) |
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
| A. | 若直线a与平面α内无数条直线平行,则a∥α | |
| B. | 经过两条异面直线中的一条,有一个平面与另一条直线平行 | |
| C. | 平行于同一平面的两条直线平行 | |
| D. | 直线a,b共面,直线a,c共面,则直线b,c共面 |
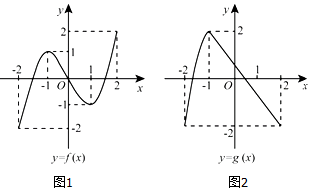
| A. | 函数f[g(x)]的零点有且仅有6个 | B. | 函数g[f(x)]的零点有且仅有3个 | ||
| C. | 函数f[f(x)]的零点有且仅有5个 | D. | 函数g[g(x)]的零点有且仅有4个 |