已知函数y=f在[-2.2]上的图象如图所示.给出下列四个选项同.其中不正确的是( )A．函数f[g(x)]的零点有且仅有6个B．函数g[f(x)]的零点有且仅有3个C．函数f[f(x)]的零点有且仅有5个D．函数g[g(x)]的零点有且仅有4个题目和参考答案——青夏教育精英家教网—

题目内容

7．已知函数y=f（x）和y=g（x）在[-2，2]上的图象如图所示，给出下列四个选项同，其中不正确的是（　　）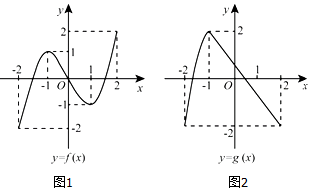

	A．	函数f[g（x）]的零点有且仅有6个		B．	函数g[f（x）]的零点有且仅有3个
	C．	函数f[f（x）]的零点有且仅有5个		D．	函数g[g（x）]的零点有且仅有4个

分析把复合函数的定义域和值域进行对接，看满足外层函数为零时内层函数有几个自变量与之相对应即可判定

解答解：∵在y为[-2，-1]时，g（x）有两个自变量满足，在y=0，y为[1，2]时，g（x）同样都是两个自变量满足，∴A正确
∵f（x）值域在[-1，2]上都是一一对应，而在值域[0，1]上都对应3个原像，∴B错误
同理可知C、D正确
故选：B．

点评本题考查了复合函数的对应问题，做题时注意外层函数的定义域和内层函数值域的对接比较．属于难题．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

18．已知角α的顶点在原点，始边与x轴正半轴重合，点P（-4，3）是角α终边上一点，则sinα+2cosα=-1．

15．设函数$f（x）=4sinx•{sin^2}（{\frac{π}{4}+\frac{x}{2}}）+cos2x$，若|f（x）-m|＜2成立的充分条件是$\frac{π}{6}≤x≤\frac{2π}{3}$，则实数m的取值范围为（0，5）．

2．今有一组实验数据，如表：

x	1.993	3.002	4.001	5.032	6.121
y	1.501	4.413	7.498	12.04	17.93

现准备从以下函数中选择一个最能代表两个变量x、y之间的规律，则拟合最好的是（　　）

A．

y=2^x-1+1

B．

$y=\frac{3}{2}{log_2}x$

C．

$y=\frac{1}{2}{x^2}-\frac{1}{2}$

D．

y=-2x-2

12．设a为实数，函数f（x）=2x²+（x-a）•|x-a|．
（1）求f（x）的最小值；
（2）设h（x）=f（x）_min，x∈（a，+∞），求不等式h（x）≥1的解集．

19．已知集合A={x|1＜x≤3}，B={x|x＜4，x∈Z}，则A∩B=（　　）

16．对于函数f（x）定义域中任意的x₁，x₂（x₁≠x₂），有如下结论：
①f（x₁+x₂）=f（x₁）•f（x₂）；
②f（x₁•x₂）=f（x₁）•f（x₂）；
③f（$\frac{{x}_{1}{+x}_{2}}{2}$）＞$\frac{f{（x}_{1}）+f{（x}_{2}）}{2}$；
④$\frac{f{（x}_{1}）-f{（x}_{2}）}{{x}_{1}{-x}_{2}}$＞0；
⑤当1＜x₁＜x₂时$\frac{f{（x}_{1}）}{{x}_{1}-1}＞\frac{f{（x}_{2}）}{{x}_{2}-1}$；
当f（x）=${（\frac{3}{2}）}^{x}$时，上述结论中正确结论的序号是①④⑤．

17．集合P={x||x|＞1}，Q={x|y=$\sqrt{4-{x}^{2}}$}，则P∩Q=（　　）

试题分类