题目内容
已知tan（α+β）=
，tan（α+
）=
，则tan（β-
）= ．
| 2 |
| 5 |
| π |
| 4 |
| 3 |
| 22 |
| π |
| 4 |
考点：两角和与差的正切函数
专题：三角函数的求值
分析：由三角函数的公式可得tan（β-
）=tan[（α+β）-（α+
）]=
，代入已知数据化简可得．
| π |
| 4 |
| π |
| 4 |
tan(α+β)-tan(α+
| ||
1+tan(α+β)tan(α+
|
解答：
解：∵tan（α+β）=
，tan（α+
）=
，
∴tan（β-
）
=tan[（α+β）-（α+
）]
=
=
=
，
故答案为：
．
| 2 |
| 5 |
| π |
| 4 |
| 3 |
| 22 |
∴tan（β-
| π |
| 4 |
=tan[（α+β）-（α+
| π |
| 4 |
=
tan(α+β)-tan(α+
| ||
1+tan(α+β)tan(α+
|
=
| ||||
1+
|
| 1 |
| 4 |
故答案为：
| 1 |
| 4 |
点评：本题考查两角差的正切公式，角的整体代入是解决问题的关键，属基础题．
练习册系列答案
相关题目
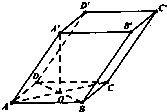如图四棱柱ABCD-A′B′C′D′的底面是正方形，O是底面的中心，A′O=1，AB=AA′=A′D=A′B=