题目内容
求出函数y=cosx,x∈[-
,
]的最小值及最大值.
| π |
| 3 |
| π |
| 2 |
考点:余弦函数的图象
专题:三角函数的图像与性质
分析:根据余弦函数的图象即可得解.
解答:
解:∵x∈[-
,
]
∴由余弦函数的图象可知:cosx∈[0,1]
∴函数y=cosx,x∈[-
,
]的最小值是0,最大值是1.
| π |
| 3 |
| π |
| 2 |
∴由余弦函数的图象可知:cosx∈[0,1]
∴函数y=cosx,x∈[-
| π |
| 3 |
| π |
| 2 |
点评:本题主要考查了余弦函数的图象和性质,属于基础题.

练习册系列答案
相关题目
设F为双曲线C:
-
=1(a>0,b>0)的右焦点,过点F且斜率为-1的直线l与双曲线C的两条渐近线分别交于A,B两点,若
=-3
,则双曲线C的离心率e=( )
| x2 |
| a2 |
| y2 |
| b2 |
| AB |
| AF |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数f(x)=Asin(ωx+φ)( A>0,ω>0,|φ|<
)的部分图象如图所示,则φ=( )
| π |
| 2 |

A、
| ||
B、
| ||
C、-
| ||
D、-
|
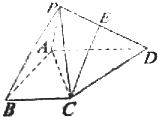 如图所示,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面所成的角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,PA=BC=
如图所示,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面所成的角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,PA=BC=